Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 3.Problemas - Ex. 9

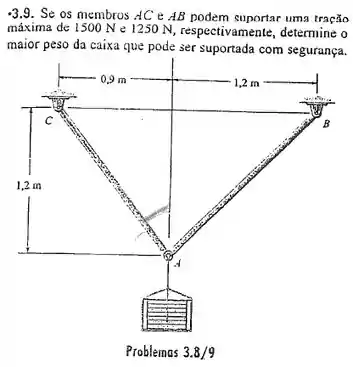
Passo 1

Vamos fazer o diagrama de corpo livre do nó A :

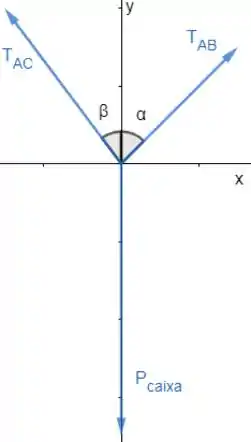
Podemos descobrir alpha e beta usando as relações trigonométricas:

t a n g e n t e = (c a t e t o o p o s t o)/(c a t e t o a d j a c e n t e)

tg beta = (0,9)/(1,2)

tag beta = (3)/(4)

Perceba que esse ângulo faz parte de um triângulo 3, 4, 5. Então

sen beta = (3)/(5) e cos beta = (4)/(5)

beta tildetilde 36,9 °

tg alpha = (1,2)/(1,2)

alpha = 45 °

Passo 2

A soma de forças em x e em y deve ser zero.

Vamos decompor primeiro as forças em x , pois dessa forma vamos encontrar uma relação entre T_A B e T_A C :

sum F_x = 0

T_A B sen alpha - T_A C sen beta = 0

T_A B sen 45 ° - T_A C sen beta = 0

T_A B = (T_A C sen beta)/(sen 45 °)

T_A B = (T_A C ( 3 // 5 ))/(( sqrt(2) // 2 ))

T_A B = (3 sqrt(2))/(5) * T_A C

Se a barra AB suportar sua tração máxima:

1250 = (3 sqrt(2))/(5) * T_A C

T_A C = 1250 * ((5)/(3 sqrt(2)))

T_A C = 1473 N

Portanto quando AB entiver suportando o máximo de força a barra AC ainda não vai ter chegado no seu limite. Essa é a situação que vamos observar, pois se aumentarmos a tração na barra AC para chegar ao máximo dela, a barra AB vai se romper por estar submetida a uma carga maior do que ela suporta.

Passo 3

Agora vamos decompor as forças em y :

sum F_y = 0

T_A C cos beta + T_A B cos alpha - P_c a i x a = 0

P_c a i x a = T_A C cos beta + T_A B cos alpha

Sabemos o valor de alpha , de cos beta , de T_A C e de T_A B , vamos substituir tudo na equação:

P_c a i x a = (1473) ((4)/(5)) + (1250) cos 45

P_c a i x a = 2062 N

Resposta

P_c a i x a = 2062 N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas hastes estão ligadas por um bloco deslizante como mostra a figura. Desprezando o efeito do atrito, determine o binário M a necessário para manter o sistema em equilíbrio.
O braço A B C está ligado por pinos ao colar em B e à manivela C D em C . Desprezando o efeito do atrito, determine o binário M necessário para manter o sistema em equilíbrio quando θ = 0 ° .
A haste C D está presa ao colar D e passa por um colar soldado na extremidade B da alavanca A B . Desprezando o efeito do atrito, determine o binário M necessário para manter o sistema em equilíbrio q
Dois cilindros hidráulicos controlam a posição do braço robótico A B C . Na posição mostrada na figura os cilindros estão paralelos, determine a força exercida em cada cilindro quando P = 160 N e Q =
Duas hastes estão ligadas por um bloco deslizante como mostra a figura. Desprezando o efeito do atrito, determine o binário M a necessário para manter o sistema em equilíbrio.