Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas fundamentais - Ex. 08
O disco de 50 kg está submetido ao momento de binário M = (9t) N.m, onde t é dado em segundos. Determine a velocidade angular do disco quando t = 4 s partindo do repouso.
Passo 1
Para a resolução desse exercício, iremos adotar . Primeiramente iremos calcular o momento de inércia do disco em relação ao ponto O:
Passo 2
Agora iremos aplicar o somatório de momento em torno do ponto O com o auxílio da imagem a seguir para obter o valor da aceleração angular em função do tempo:
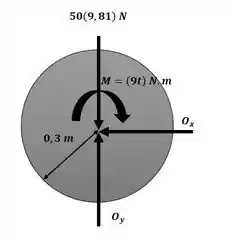
Passo 3
Sabemos que a aceleração é a derivada da velocidade no tempo, sendo assim:
Resposta
Exercícios de Livros Relacionados
O avião a jato tem uma massa de 22Mg e um centro de massa em G. Se um cabo de rebocar está fixado à parte superior do trem de pouso do nariz e exerce uma força T = 400N , como mostrado, determine a ac
A empilhadeira manual tem uma massa de 70 kg e centro de massa em G. Se ela levanta a bobina de 120 kg com uma aceleração de 3 m/s², determine as reações em cada uma das quatro rodas. A carga é simétr
A figura mostra a vista lateral da estrutura das rodas (truque) de um vagão de passageiros onde a carga vertical é transmitida à estrutura em que os assentos dos mancais das rodas estão localizados. A
Uma biela é sustentada por um fio de faca no Ponto A; o período de suas pequenas oscilações é observado como 0,87 s. A haste é então invertida e suportada por um fio de faca no Ponto B e o período de
O compressor mostrado tem uma massa de 250 kg e opera a 2.000 rpm. Nesta condição de operação, vibração indesejável ocorre quando o compressor é acoplado diretamente ao solo. Para reduzir a vibração d