Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 29

A empilhadeira manual tem uma massa de 70 kg e centro de massa em G. Se ela levanta a bobina de 120 kg com uma aceleração de 3 m/s², determine as reações em cada uma das quatro rodas. A carga é simétrica. Despreze a massa do braço móvel CD.

Passo 1

Antes de iniciar o exercício, devemos notar que temos dois pontos de apoio em A e outros 2 em B, isso será importante na hora de aplicar os somatórios de momento e de força. Para a resolução desse exercício, iremos adotar a aceleração da gravidade local g = 9,81 m/s².

Passo 2

Para determinar as reações nas rodas no ponto A, faremos um somatório de momento em torno do ponto B com o auxílio do esquema a seguir. adotando o sentido anti-horário como positivo:

↺ + ∑ M B = ∑ M k B

70 9,81 0,5 + 120 9,81 0,7 - 2 N A 1,25 = - ( 120 ) ( 3 ) ( 0,7 )

N A = 567,76   N

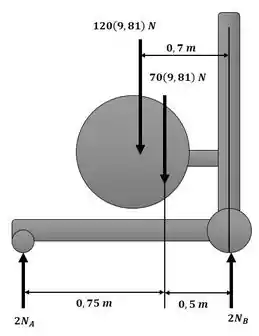
Passo 3

Por fim, encontraremos a força normal de reação no ponto B fazendo um somatório de forças no eixo y:

+ ↑ ∑ F y = m . a G y

2 567,76 + 2 N B - 120 9,81 - 70 ( 9,81 ) = 120 ( 3 )

N B = 544   N

Resposta

N A = 567,76   N

N B = 544   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A empilhadeira e o operador têm uma massa combinada de 5000 kg e o centro de massa em G. Se a empilhadeira é usada para erguer o cano de concreto de 1000 kg, determine as reações normais sobre cada um
A empilhadeira e o operador têm uma massa combinada de 5000 kg e o centro de massa em G. Se a empilhadeira é usada para erguer o cano de concreto de 1000 kg, determine a aceleração vertical máxima que
A empilhadeira se desloca para frente com uma velocidade constante de 2,7 m/s. Determine a distância de parada mais curta sem fazer com que nenhuma das rodas deixe o solo. A empilhadeira tem massa de
Cada caixa uniforme na pilha de quatro caixas tem uma massa de 4 kg. A pilha está sendo transportada em um carrinho que tem uma massa de 15 kg. Determine a força máxima F que a mulher pode exercer sob
O braço BDE do robô industrial é ativado aplicando-se o torque M = 50 N.m ao membro CD. Determine as reações nos pinos B e D quando os membros estão na posição mostrada e têm uma velocidade angular de