Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas fundamentais - Ex. 10

No instante mostrado, o disco de 30 kg tem uma velocidade angular no sentido anti-horário de ω = 10   r a d / s . Determine as componentes normais e tangenciais da reação do pino O sobre o disco e a aceleração angular do disco nesse instante.

Passo 1

Para a resolução desse exercício, iremos adotar g = 9,81   m / s 2 . Primeiramente iremos escrever as componentes normal e tangencial da aceleração com o auxílio da imagem a seguir:

a G n = ω 2 r G = 10 2 0,3 → a G n = 30   m / s 2

a G t = α r G = α 0,3

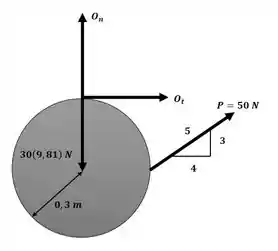
Agora iremos calcular o momento de inércia do disco em torno do ponto O:

I O = 1 2 m r 2 + m d 2 = 1 2 30 0,3 2 + 30 0,3 2 → I O = 4,05   k g . m 2

Passo 2

Com isso, podemos aplicar o somatório de momentos em relação ao ponto O com o auxílio do diagrama apresentado no passo 1:

↺ + ∑ M O = I O α

50 3 5 0,3 + 50 4 5 0,3 = 4,05 α

α = 5,19   r a d / s 2

Passo 3

Agora podemos aplicar o somatório de forças na direção normal para obter o valor da sua reação:

+ ↑   ∑ F n = m a G n

O n + 50 3 5 - 30 9,81 = 30 30 → O n = 1164,3   N

E agora, na direção tangencial:

+ →   ∑ F t = m a G t

O t + 50 4 5 = 30 5,185 0,3

O t = 6,67   N

Resposta

O n = 1164,3   N

O t = 6,6 7   N

α = 5,19   r a d / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

115. A nave espacial apresentada é simétrica em relação a seu eixo z e possui um raio de giração de 720m m em relação a esse eixo. Os raios de giração em relação aos eixos x e y através do centro de m
122. Um projétil que se desloca através da atmosfera com uma velocidade v - que faz um pequeno ângulo θ com seu eixo geométrico é submetido a uma força aerodinâmica resultante R essencialmente no sent
123. O disco circular maciço de massa m e pequena espessura está girando livremente sobre seu eixo à taxa p . Se o conjunto é liberado na posição vertical em θ = 0 com θ ˙ = 0 , determine as component
106. As pás e o cubo do rotor do helicóptero têm uma massa de 64k g e um raio de giração de 3,0m em relação ao eixo de rotação z . Com o rotor girando a 500r p m durante um curto intervalo após a deco
98. A estudante se ofereceu voluntariamente para auxiliar em uma demonstração na sala de aula envolvendo uma roda com quantidade de movimento, que está girando rapidamente com velocidade angular p com