Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.6 - Ex. 43

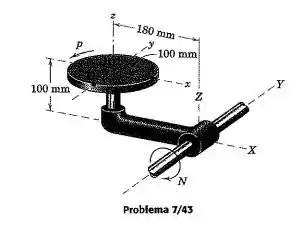
O disco circular com 100 mm de raio gira em torno de seu eixo z com a velocidade constante p = 240   r p m , e o braço O C B gira em torno do eixo Y na velocidade constante N = 30   r p m . Determine a velocidade v e a aceleração a do ponto A sobre o disco quando passa pela posição mostrada. Utilize os eixos de referência x - y - z presos ao braço O C B .

Passo 1

Para resolvermos o problema, usaremos as relações de velocidade e aceleração de um ponto dadas no livro. Também converteremos os valores para deixar no sistema SI para facilitar nossas contas.

Passo 2

Vamos começar estabelecendo os pontos O e B . B será em r O B = - 0.18 ⋅ i ^ + 0.1 ⋅ j ^   m e A será em r A B = 0.1 ⋅ j ^   m , usando agora B como ponto de referência para A . Dessa forma, podemos usar a relação dada de:

v A = v B + Ω × r A B + v r e l

Precisamos agora descobrir as grandezas Ω ,   v b   e   v r e l . Temos que v r e l será a velocidade do ponto A para alguém preso no centro de x - y - z . Portanto, v r e l = p ⋅ k ^ × r A B . Convertendo p de rpm para m/s, temos que:

p = 240   r p m = 240 ⋅ 2 ⋅ π 60 = 8 ⋅ π   r a d / s

Assim, v r e l = 8 ⋅ π ⋅ k ^ r a d / s × 0.1 ⋅ j ^   m = 0.8 ⋅ π ⋅ j ^   m / s

Temos que Ω será a velocidade angular dos eixos. Assim, o mesmo será dado por:

Ω = 2 ⋅ π ⋅ 30   r p m 60 ⋅ j ^ = π ⋅ j ^   r a d / s

Calculando agora v B , temos que o mesmo será dado por:

v B = Ω × r O B = π ⋅ j ^ r a d / s × - 0.18 ⋅ i ^ + 0.1 ⋅ j ^   m = π ⋅ 0.1 ⋅ i ^ + 0.18 ⋅ k ^   m / s  

E por fim, temos Ω × r A B = π ⋅ j ^ r a d / s × 0.1 ⋅ i ^   m = - 0.1 ⋅ π ⋅ k ^

Agora, substituindo todos os valores na equação da velocidade, teremos que:

v A = π ⋅ 0.1 ⋅ i ^ + 0.8 ⋅ j ^ + 0.08 ⋅ k ^   m / s

Para encontrarmos a aceleração, usaremos outra relação dada que se encontra derivando a relação da velocidade. Temos então que:

a A = a B + Ω ˙ × r A B + Ω × Ω × r A B + 2 ⋅ Ω × v r e l + a r e l

Onde:

a B = Ω × Ω × r O B = π 2 ⋅ 0.18 ⋅ i ^ - 0.1 ⋅ k ^   m / s 2 .

Ω × Ω × r A B = π ⋅ j ^ × - 0.1 ⋅ π ⋅ k ^ = ( 0.1 ⋅ π 2 ⋅ i ^ )   m / s 2

2 ⋅ Ω × v r e l = 2 ⋅ π ⋅ j ^ × 0.8 ⋅ π ⋅ j ^ = 0

a r e l = p ˙ ⋅ k ^ × r A B + r A B ⋅ p 2 ⋅ - i ^ = 0 - 8 ⋅ π 2 ⋅ 0.1 ⋅ i ^ = - 6.4 ⋅ π 2 ⋅ i ^   m / s 2

Ω ˙ × r A B = 0 × - 0.1 ⋅ π ⋅ k ^ = 0

Assim, temos que a aceleração final será:

a A = - 0.1 ⋅ π 2 ⋅ i ^ m / s 2 - 6.4 ⋅ π 2 ⋅ i ^ m / s 2 + π 2 ⋅ 0.18 ⋅ i ^ - 0.1 ⋅ k ^ m / s 2

a A = - π 2 ⋅ 6.32 ⋅ i ^ + 0.1 ⋅ k ^ m / s 2

Resposta

Resposta: v A = π ⋅ 0.1 ⋅ i ^ + 0.8 ⋅ j ^ + 0.08 ⋅ k ^   m / s

a A = - π 2 ⋅ 6.32 ⋅ i ^ + 0.1 ⋅ k ^   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A bobina A gira em torno de seu eixo com uma velocidade angular de 20rad/s, inicialmente no sentido de w0 e em seguida no sentido de ws. Simultaneamente, o conjunto gira em torno do eixo vertical com
Um disco circular gira em torno de um eixo fixo com uma velocidade angular constante ω =10 i + 2 j + 2 k r a d / s . Em um determinado instante, um ponto P sobre sua borda possui uma velocidade cujas
O conjunto de painéis e os eixos vinculados x-y-z giram com uma velocidade angular constante Ω = 0,6r a d / s em torno do eixo vertical z. Simultaneamente, os painéis giram em torno do eixo y como mos
Se o motor gira em torno do eixo x na taxa constante γ ˙ = 3 π r a d / s , sem rotação em torno do eixo Z, determine a aceleração angular do rotor e do disco no instante em que a posição γ = 30 ° é cr
Enquanto manipula o haltere, as garras do dispositivo robótico possuem uma velocidade angular de 2 rad/s em torno do eixo OG com γ = 60 ° . O conjunto inteiro gira em torno do eixo vertical Z na taxa