Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.8 - Ex. 62

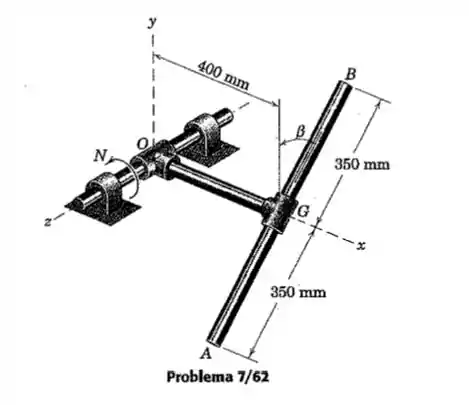
A barra de aço esbelta AB possui uma massa de 2.8 kg e está ligada ao eixo que gira pela barra OG e suas conexões em O e G. O ângulo β permanece constante em 30º, e todo o conjunto rígido gira em torno do eixo z na taxa constante N=600 rpm. Calcule a quantidade de movimento angular H 0 de AB e sua energia cinética T.

Passo 1

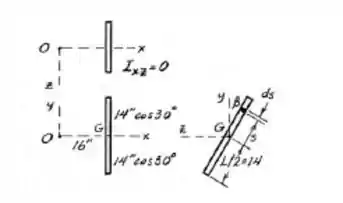
Para esse problema nós não teremos componentes da velocidade angular em x e nem em y ( ω x = ω y = 0 ) .

Pela regra da mão direita nós teremos ω z = N k ^

Da equação 7/11 nós teremos.

H o = ω z ( - I x z i ^ - I y z j ^ + I z z k ^ )

ω z = 600 * 2 π 60 r a d s = 20 π r a d s

Passo 2

I x z = ∫ - x z d m = 0 devido a coordenada x sempre ficar fixa e girar em torno de z

I y z = ∫ - y z d m = ∫ - l 2 l 2 ( s * cos ⁡ β * ( - s * sin ⁡ β ) ρ d s Sendo ρ = m l densidade linear de massa

= - ρ l 3 24 s e n ( 2 β )

I y z = - 2.8 0.7 * s e n 60 0.7 3 24 = 0.05   k g * m 2

I z z = 1 12 m l 2 + m d 2 momento de um cilindro em torno do diâmetro central.

I z z = 1 12 * ( 2.8 * 0.7 c o s 30 2 + 2.8 * 0.4 2 = 0.14   k g * m 2

H o = - 0.05 j ^ - 0.14 k ^ 20 π = ( - 3.1 j ^ + 8.9 k ^   ) k g * m 2 s

Passo 3

A energia cinética é dada pela equação 7/18

T = 1 2 ω * H o = - 3.1 j ^ + 8.9 k ^   * 20 π k ^ = 559.2   J a u l e s

Resposta

H o = ( - 3.1 j ^ + 8.9 k ^   ) k g * m 2 s

T = 559.2   J a u l e s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O braço BDE do robô industrial é ativado aplicando-se o torque M = 50 N.m ao membro CD. Determine as reações nos pinos B e D quando os membros estão na posição mostrada e têm uma velocidade angular de
O carrinho de mão tem uma massa de 200 kg e centro de massa em G. Determine as reações normais em cada uma das duas rodas em A e em B se uma força de P = 50 N for aplicada à alça. Despreze a massa das
O carrinho de mão tem uma massa de 200 kg e centro de massa em G. Determine a maior intensidade da força P que pode ser aplicada à alça de maneira que as rodas em A ou B continuem a manter contato com
Se as rodas traseiras da empilhadeira fornecerem uma força de tração combinada de F A = 1500N , determine a sua aceleração e as reações normais sobre os pares de rodas traseiras e dianteiras. A empilh
A caixa uniforme tem uma massa de 50 kg e repousa sobre o carrinho tendo uma superfície inclinada. Determine a menor aceleração que vai fazer com que a caixa tombe ou deslize em relação ao carrinho. Q