Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.11 - Ex. 117

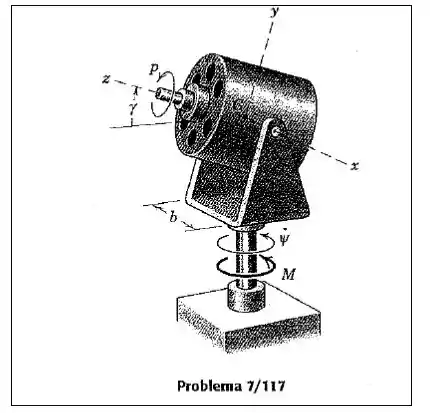
A carcaça de um motor elétrico é livremente articulado em torno do eixo horizontal x, que passa através do centro de massa G do rotor. Se o motor está girando a taxa constante de ϕ ˙ = p , determine a aceleração angular ψ ¨ que resultará da aplicação do momento M sobre o eixo vertical γ ˙ = ψ ˙ = 0 . A massa da estrutura e da carcaça é considerada desprezível comparada com a massa m do rotor. O raio de giração do rotor em relação ao eixo z é K z e em relação ao eixo x é K x .

Passo 1

Definir as equações de equilíbrio:

I = m K z ²

I o = m K x 2

γ = π ² -   θ

↺ + Σ M Z = - F y . b = m K z ² d d t ( ψ ¨ s i n γ + p )

↺ + Σ M X = I o = θ ¨ - 0 + 0 ;   θ ¨ = ψ ¨ = 0

↺ + Σ M Y = F c = F z . b = m K x ²   ( ψ ¨ c o s   γ )

Passo 2

Agora isolando Fy:

- F y . b = m K z ² d d t ( ψ ¨ s i n γ + p )

E substituindo na equação de momento abaixo:

M = F z . b . c o s γ - F y . b . s i n γ

Passo 3

Obteremos:

ψ ¨ = M / m K x ² . c o s ² γ + K z ² . s i n ² y

Resposta

Assim a aceleração angular será de:

M / m K x ² . c o s ² γ + K z ² . s i n ² y

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o momento fletor M no ponto de tangência A na barra semicircular de raio r e massa m , enquanto a barra gira em torno do eixo tangente com uma velocidade angular constante e elevada ω . Desp
Resolva o Probl. 7/85 para o caso em que o conjunto parte do repouso com uma aceleração angular inicial α = 900r a d / s 2 como resultado de um torque de partida(binário) M aplicado á haste no mesmo s
A haste esbelta de massa m e comprimento L está montada em um mandril que gira com o eixo da haste desalinhado em relação ao eixo z de rotação pelo ângulo β . Determine o momento fletor M O na base O
Se a placa triangular homogênea do Prob. 7/92 é liberada a partir do repouso na posição mostrada, determine o módulo da reação no mancal em A após a placa ter girado 90º.
A grande antena para rastreamento de satélite possui um momento de inércia I em relação a seu eixo z de simetria e um momento de inércia I o em relação a cada um dos eixos x e y . Determine a aceleraç