Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 32
O dragster tem uma massa de 1500 kg e um centro de massa em G. Se não ocorre nenhum deslizamento, determine a força de atrito que tem de ser desenvolvida em cada uma das rodas motrizes traseiras B a fim de criar uma aceleração . Quais são as reações normais de cada roda sobre o solo? Despreze a massa das rodas e suponha que as rodas dianteiras estão livres para rodar.
Passo 1
Devemos notar que temos duas rodas no ponto A e duas rodas no ponto B.
Para a resolução desse exercício, iremos adotar a aceleração da gravidade local g = 9,81 m/s².
Sendo assim, com o auxílio do diagrama de corpo livre a seguir:
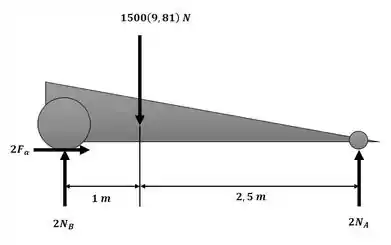
Podemos aplicar o somatório de momentos no ponto B (adotando o sentido anti-horário como positivo) para descobrir a reação no ponto A:
Passo 2
Com a reação no ponto A, podemos aplicar somatório de forças na direção y e descobrir qual é a reação de apoio no ponto B:
Passo 3
Por fim, iremos encontrar a força de atrito através do somatório de forças na direção x: