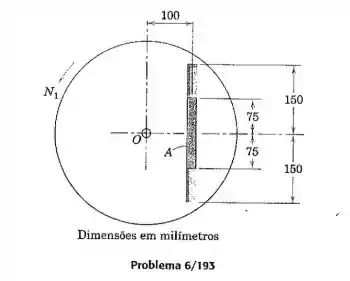
O disco circular ranhurado de tem um raio de giração em relação ao seu centro de e inicialmente está girando livremente em torno de um eixo vertical fixo através de com uma velocidade . A barra esbelta uniforme de está inicialmente em repouso em relação ao disco, na posição central da ranhura conforme mostrado. Uma leve perturbação faz com que a barra deslize para a extremiade da ranhura onde atinge o repouso em relação ao disco. Calcule a nova velocidade angular do disco, supondo a ausência de atrito no mancal do eixo em . A presença de atrito na ranhura afeta o resultado final?
Passo 1
A configuração 1 é representada na figura abaixo:
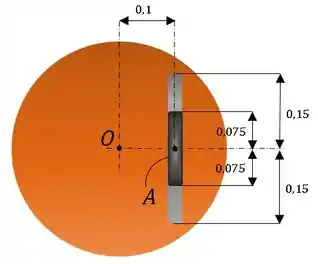
Para essa configuração, temos
Passo 2
Como o disco rotaciona no sentido anti-horário, a barra esbelta tende a deslizar para cima e atingir o repouso estando em contato com a extremidade superior da ranhura, confome a figura abaixo.
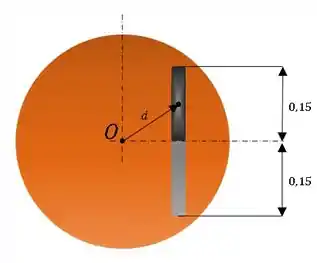
Note que a distância entre o centro de massa do disco e o centro de massa da barra esbelta na configuração 2 é dado por
Assim, ficamos com
Passo 3
Pela conservação da quantidade de movimento angular, temos
Substituindo as expressões encontradas, ficamos com
Resolvendo para , obtemos
A presença de atrito na ranhura é considerada uma força interna e, portanto, não interfere na quantidade de movimento angular. Assim, não altera a velocidade angular final do disco.