Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.8 - Ex. 61

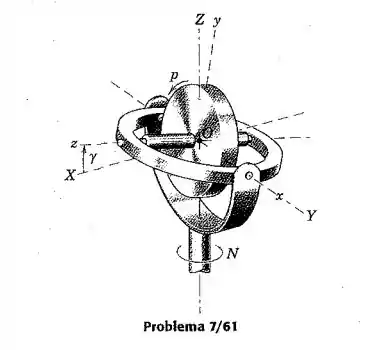
O rotor do giroscópio está girando na taxa constante p = 100   r p m em relação aos eixos x - y - z , no sentido indicado. Se o ângulo γ entre o anel de suspensão e o plano horizontal X - Y é levado a aumentar à taxa de 4   r a d / s e se a unidade é obrigada a realizar precessão em relação à vertical na taxa constante N = 20   r p m , calcule a quantidade de movimento angular H o do rotor quando γ = 30 º . Os momentos de inércia axial e transversal são I z z = 6 ⋅ 10 - 3   k g ⋅ m 2 e I x x = I y y = 3 ⋅ 10 - 3   k g ⋅ m 2 .

Passo 1

Para encontrarmos a quantidade de movimento H o para esse problema, iremos precisar calcular a velocidade angular total do sistema ω que é dada pela soma de todas as velocidades do sistema. Após isso iremos substituir na equação

H o = I x x ⋅ ω x ⋅ i + I y y ⋅ ω y ⋅ j + I z z ⋅ ω z ⋅ k

Passo 2

Vamos começar calculando a velocidade do sistema ω . Temos que ela será dada por

ω = p ⋅ k - γ ˙ ⋅ i + N = p ⋅ k - γ ˙ ⋅ i + N ⋅ cos ⁡ γ ⋅ j + sin ⁡ γ ⋅ k

Onde N é a velocidade de precessão do sistema e γ é o ângulo.

Convertendo as unidades todas para r a d / s , temos que p = 100 ⋅ 2 ⋅ π 60 = 10 ⋅ π 3   r a d / s e que N = 20 ⋅ 2 ⋅ π 60 = 2 ⋅ π 3   r a d / s . Assim, temos que

ω = 10 ⋅ π 3   r a d / s ⋅ k - 4   r a d / s   ⋅ i + 2 ⋅ π 3   ⋅ cos ⁡ 30 º ⋅ j + sin ⁡ 30 º ⋅ k   r a d / s    

ω = - 4   ⋅ i + 1.814 ⋅ j + 11.52 ⋅ k   r a d / s  

Agora queremos encontrar H o . Se substituirmos os valores dado pelo problema com os encontrados no Passo 2 na equação mostrada no Passo 1, teremos que:

H o = - 0.012 ⋅ i + 0.00544 ⋅ j + 0.0691 ⋅ k   k g ⋅ m 2 / s

Resposta

H o = - 0.012 ⋅ i + 0.00544 ⋅ j + 0.0691 ⋅ k   k g ⋅ m 2 / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O duto de concreto de 500 kg tem um raio médio de 0,5 m. Se o caminhão tem uma aceleração 3 m/s², de termine a aceleração angular do duto. Supondo que o duto não deslize sobre o piso da carroceria do
A roda de 75 kg e um raio de giração K g375m m em relação a seu centro de massa G. Se ela é submetida a um torque M=150N m Determine sua aceleração angular. Os coeficientes de atrito cinético e estáti
4. Um mecanismo de sincronização consiste no braço distribuidor A B que gira e no contato fixo C . Se o braço gira em torno do eixo fixo O A com uma velocidade angular constante ω → = 30 3 i ^ + 2 j ^
3. Repita o experimento do problema 7 / 2 , mas use um ângulo de rotação pequeno, por exemplo, 5 ° . Observe as posições finais aproximadamente iguais para as duas sequências distintas de rotação. O q
5. O eixo e o rotor estão montados em um suporte em U que pode girar em torno do eixo z com uma velocidade angular Ω . Com Ω = 0 e θ constante, o rotor possui uma velocidade angular ω → 0 = - 4 j - 3