Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.4 - Ex. 51
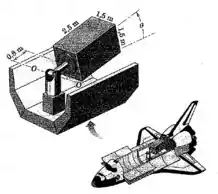
Um pedestal com uma articulação Cardan sustenta uma carga útil no ônibus espacial e a posiciona quando as portas do compartimento de carga são abertas em órbita. A carga útil é modelada como um bloco retangular homogêneo com uma massa de . O torque no eixo - da articulação Cardan é de fornecido por um motor de corrente contínua sem escovas. Com o ônibus espacial se deslocando em uma órbita “sem peso”, determine o tempo necessário para mover a carga de sua posição de alojamento em para sua posição de instalação em , se o torque é aplicado durante os primeiros do curso e então invertido nos restantes para fazer a carga parar )
Passo 1
Para poupar esforços, vamos lembrar de uma propriedade importante: o tempo que uma aceleração leva para aumentar a velocidade de zero até um certo valor é igual ao tempo que ela levaria para reduzir a velocidade desse mesmo valor até o zero.
Isso quer dizer que só precisamos calcular o tempo que a aceleração angular leva para mover o corpo por um ângulo a partir do repouso, porque em seguida o tempo de parada será o mesmo :
E o tempo total será:
Passo 2
Só falta encontrar a aceleração angular , que pode ser calculada usando a seguinte equação:
Como já temos o momento , só falta calcular o momento de inércia da carga, que foi modelada como um bloco retangular homogênio de , com uma massa de .
Em relação ao centro de massa do bloco, o momento de inércia é (consulte uma tabela):
E podemos usar o teorema dos eixos paralelos para calcular o momento de inércia quando tomamos o eixo - como referência:
Sendo que é a distância entre os dois eixos, que pode ser encontrada só olhando o desenho:
Então:
Passo 3
Agora é só substituir na equação que encontramos antes:
E o tempo será:
Onde convertemos .
Resposta
O tempo necessário é de .