Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 20.Problemas - Ex. 6

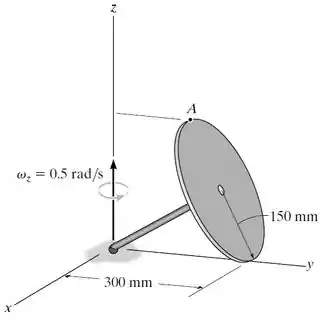
O disco gira em torno do eixo z w z = 0,5   r a d / s sem deslizar no plano horizontal. Se nesse mesmo instante w z está aumentando a ω ˙ z = 0,3   r a d / s 2 , determine a velocidade e a aceleração do ponto A no disco.

Passo 1

Como o disco gira sem escorregar, sua velocidade angular é sempre direcionada ao longo do eixo instantâneo de velocidade zero (eixo y) e pode ser expressa como:

ω = ω s + ω z

- ω j = ( - ω s cos ⁡ 30 ° j - ω s sin ⁡ 30 °   k ) + ( 0,5 k )

Equacionando as componentes j e k:

0 = - ω s sin ⁡ 30 ° + 0,5 - ω = - ω s cos ⁡ 30 °

Solucionando o sistema temos que :

ω =   0,866   r a d / s

ω s = 1   r a d / s

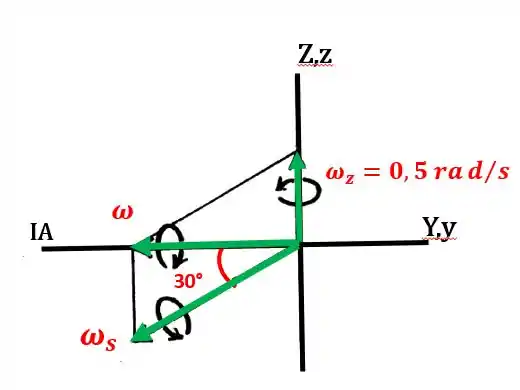
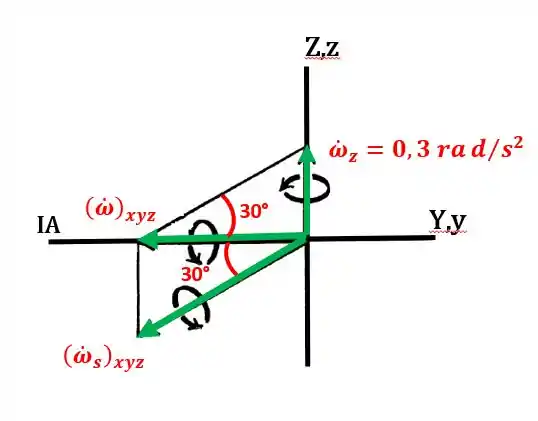
Passo 2

Como ω sempre fica no plano X-Y fixo, ω = - 0,866 j r a d / s observa-se que ele tem uma direção constante a partir de xyz em rotação, logo , Ω = ω z = 0,5 k r a d / s .

ω ˙ s x y z = - 0,3 sin ⁡ 30 ° ( cos ⁡ 30 ° ) j - 0,3 sin ⁡ 30 ° sin ⁡ 30 ° k =   [ - 0,5196 j - 0,3 k ] r a d / s 2

Assim:

ω ˙ x y z = ω ˙ z + ω ˙ x x y z = - 0,5196 j   r a d / s 2

Sendo a aceleração angular dada pela equação abaixo, temos:

α = ω = ˙ ω ˙ x y z + ω z × ω

α = ( - 0,5196 j ) + ( 0,5 k ) × ( 0,866 j )

α = 0,4330 i - 0,5196 j   r a d / s 2

Passo 3

Para o cálculo da velecidade e aceleração escalares é necessário saber as componentes da distância OA, desse modo :

r A = 0,3 - 0,3 cos ⁡ 60 ° j + 0,3 sin ⁡ 30 ° k = [ 0,15 j + 0,2598 k ] m

Logo a velocidade será:

v A = ω × r A = - 0,866 j   × 0,15 j + 0,2598 k = - 0,225 i m / s

E a aceleração será:

a A = α × r A + ω × ( ω × r A )  

a A = 0,4330 i - - 0,5196 j × 0,15 j + 0,2598 k + - 0,866 j   × [ - 0,866 j   × 0,15 j + 0,2598 k ]

a A = - 0,135 i - 0,1125 j - 0,130 k m / s 2

Resposta

De acordo com os passos 1, 2 e 3 a velocidade e a aceleração do ponto A no disco serão respectivamente :

v A = - 0,225 i m / s

a A = - 0,135 i - 0,1125 j - 0,130 k m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para as condições do prob. 5/173 obtenha a expressão vetorial para a aceleração que a aeronave A aparenta ter para um observador interior de B e girando com a aeronave B, na qual os eixos x-y estão fi
Os carros A e B estão contornando as curvas com velocidades iguais 72 km/h. Determine a velocidade que A parece ter para um observador se deslocando e girando com o carro B para o instante representad
Um edifício alto está situado sobre o equador. O lado norte do edifício aloja um relógio de 12 horas comum cujo centro está a uma distância h acima do chão (que está aproximadamente ao nível do mar).
O caminhão de bombeiros está se deslocando para frente a uma velocidade de 60 km/h e está desacelerando na taxa de 3 m/s². Simultaneamente, a escada está sendo elevada e prolongada. No instante consid
Para o instante representado, a barra CB está girando no sentido anti-horário a uma taxa constante N = 4r a d / s , e seu pino A provoca uma rotação sentido horário do membro ranhurado ODE. Determine