Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 20.Problemas - Ex. 3

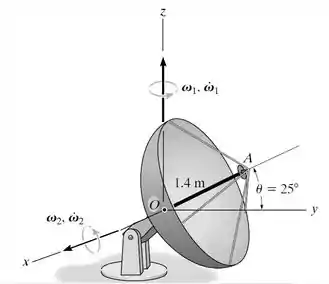
Em um dado instante, o disco da antena de satélite tem um movimento angular w 1 = 6   r a d / s e w ˙ 1 = 3   r a d / s 2   em torno do eixo z. Nesse mesmo instante θ = 25 ° , o movimento angular em torno do eixo x é w 2 = 2   r a d / s , e w ˙ 2 = 1,5   r a d / s 2 . Determine a velocidade e a aceleração do mastro receptor A nesse instante.

Passo 1

A velocidade angular pode ser expressa na forma de um vetor cartesiano, por meio da soma das componentes das velocidades ω 1 e ω 2 , de mode que :

ω = ω 1 + ω 2 = 2 i + 6 k   r a d / s

Passo 2

A aceleração angular será:

α = ω ˙ = ω ˙ 1 + ω ˙ 2 (1)

Para ω 2 , Ω = ω 1 = 6 k   r a d / s   , então:

ω ˙ 2 = ω ˙ 2 x y z + ω 1 × ω 2 = 1,5 i + 6 k × 2 i

ω ˙ 2 = ω ˙ 2 x y z + ω 1 × ω 2 = 1,5 i + 6 k × 2 i

ω ˙ 2 = 1,5 i + 12 j     r a d / s 2 (2)

Para ω 1 , Ω = 0   , então:

ω ˙ 1 = ω ˙ 1 x y z + 0 × ω 1 = 3 k   r a d / s 2 (3)

Substituindo (2) e (3) em (1), a aceleração angular será:

α = ω ˙ 1 + ω ˙ 2 = ( 3 k )+( 1,5 i + 12 j )

α = 1,5 i + 12 j   + 3 k     r a d /   s 2

Passo 3

Para o cálculo da velecidade e aceleração escalares é necessário saber as componentes da distância AO, desse modo :

r A = 1,4 cos ⁡ 25 ° j + 1,4   sin ⁡ 25 ° k m = [ 1,2688 j + 0,591 k ] m

Logoa a velocidade será:

v A = ω × r A = ( 2 i + 6 k ) × ( 1,2688 j + 0,591 k )

v A = - 7,61 i - 1,18 j + 2,54 k   m / s

E a aceleração será:

a A = α × r A + ω × ( ω × r A )

a A = 1,5 i + 12 j   + 3 k × 1,2688 j + 0,591 k + 2 i + 6 k × [ ( 2 i + 6 k 0 × ( 1,2688 j + 0,591 k ) ]

a A = 10,4   i - 51,6   j - 0,463   k   m / s 2

Resposta

De acordo com os passos 1, 2 3 e 4 a velocidade e a aceleração do mastro receptor A no instante descrito, serão respectivamente :

v A = - 7,61 i - 1,18 j + 2,54 k   m / s

a A = 10,4   i - 51,6   j - 0,463   k   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere o trilho de uma estrada de ferro reta e horizontal com um vagão ferroviário de 50000kg se deslocando ao longo da linha férrea a uma velocidade constante de 15m/s. Determine a força horizonta
Um veículo A viaja para o oeste em alta velocidade em uma estrada perfeitamente reta B que é tangente à superfície da Terra no equador. A estrada não possui qualquer curvatura no plano vertical. Deter
Ao contornar uma curva sem inclinação lateral a uma velocidade constante de 25 km/h, o centro C do vagão ferroviário segue uma trajetória circular de raio ρ = 60 m . O eixo longitudinal do vagão perma
Um veiculo experimental A viaja com velocidade constante v em relação à Terra ao longo de uma estrada de ferro ligando norte ao sul. Determine a aceleração de Coriolis a c o r em função da latitude θ
O carro B está contornando a curva com uma velocidade constante de 54 km/h, e o carro A está se aproximando do carro B no cruzamento com uma velocidade constante de 72 km/h. Determine a velocidade que