Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 6.Problemas - Ex. 123
O disco homogêneo de massa está em repouso sobre as superfícies de apoio em ângulo reto mostradas. A força trativa na corda é aumentada bem gradualmente desde zero. Se o atrito, tanto em quanto em , é caracterizado por , o que acontece primeiro – o disco homogêneo vai escorregar no lugar em que está ou ele começará a rolar, subido o plano inclinado? Determine o valor de para o qual esse primeiro movimento ocorre.
Passo 1
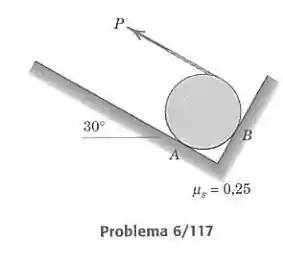
Vamos resolver essa questão por suposição. Vamos dizer que primeiro o disco irá começar a rolar em torno de antes de escorregar no lugar. Nesse caso, ele irá se descolar do ponto , e não haverão forças nesse ponto. Vamos então representar em diagrama de corpo livre o disco. Temos a normal e o atrito em , o peso e a força .
Passo 2
Primeiro, fazendo momento em torno do centro do círculo ser zero, encontramos a relação entre e a força de atrito . Vamos chamar o raio do disco de :
Agora podemos fazer a soma das forças na direção que é paralela a . O ângulo entre o peso e essa direção é de 30°.
Finalmente achamos o valor de fazendo a soma das forças na direção paralela a :
Substituímos por :
Agora vamos calcular a razão entre a normal e o atrito. Ela deve ser menor ou igual a 0,25, pois esse é o coeficiente de atrito estático:
O valor foi maior que 0,25, então nossa suposição estava errada :(
Na verdade o disco começa a escorregar no lugar antes de rolar em torno de .
Passo 3
Então vamos calcular quando o disco começa a girar no lugar. A força de atrito será máxima em e em , então será o coeficiente de atrito estático (0,25) vezes a normal em ambos os pontos. Vamos desenhar então como ficam as forças:
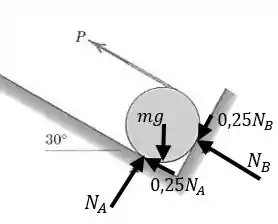
Vamos fazer as equações de força para as mesmas direções que fizemos antes. Primeiro a direção paralela a :
Colocamos então em função das outras incógnitas:
Agora na direção :
Substituímos :
Pegamos esse valor de e jogamos na expressão de , para ficar apenas em função de :
Agora vamos fazer o momento em torno do centro ser zero:
Substituímos os valores de e em função de :