Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 6.Problemas - Ex. 22
6/21) O trilho invertido com o cilindro móvel livre formam um sistema que é projetado para segurar papel ou outros materiais finos . O coeficiente de atrito estático é para todas as interfaces . Qual é o valor mínimo de que garante queo dispositivo funcionará independente do peso do material preso?
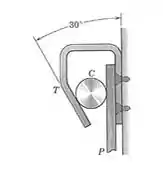
Passo 1
Então galera , como de costume , para resolvermos exercícios desse tipo será necessário aplicar as equações de equilíbrio que conhecemos .
Seja o centro da área transversal do cilindro e , assumindo que o deslizamento ocorre pimeiro no lado direito do cilindro , temos que :
Passo 2
Bo m pessoal , combinando as três equações e resolvendo o sistema linear associado a elas , nós obtemos que :
Nós assumimos e agora verificamos que o eslizamento ocorre primeiro no lado direito do cilindro .
Sendo assim , para , temos que :
Resposta
De boa galera? Então bora resolver mais exercícios como esse!