Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 17.Problemas - Ex. 8
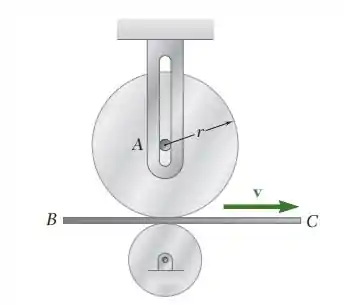
O disco A de massa 5 kg e raio r = 150 mm está em repouso quandoposto em contato com a esteira BC, que se move para a direita comvelocidade constante v = 12 m/s. Sabendo que k = 0,20 entre odisco e a esteira, determine o número de revoluções executadas pelodisco antes dele atingir uma velocidade angular constante.
Passo 1
E ai gurizada tudo belezinha???
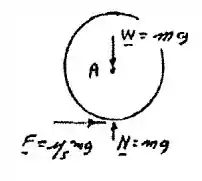
Trabalho da força de fricção externa no disco A.
Apenas a força que faz o trabalho é F. uma vez que seu momento sobre A é M = rF, temos:
Energia cinética do disco A.
A velocidade angular torna-se constante quando:
princípio de trabalho e energia para o disco A.
Mudança de Angulo:
Dadas:
Resposta
a)
Exercícios de Livros Relacionados
Referindo-se ao Problema 18.143, (a) provar que o elipsóide de Poinsot é tangente ao plano invariável, (b) mostrar que o movimento do corpo rígido deve ser tal que o elipsóide de Poinsot pareça rolar
O topo de 85 g mostrado é suportado no Ponto fixo 0. Os raios de giração do topo em relação ao seu eixo de simetria e em relação a um eixo transversal em 0 são 21 mm e 45 mm, respectivamente. Sabendo
O topo mostrado é suportado no Ponto fixo 0 e seus momentos de inércia em torno de seu eixo de simetria e em torno de um eixo transversal em 0 são denotados, respectivamente, por I e I ' . (a) Mostre
Uma esfera sólida de raio c = 3 pol. É anexada como mostrado ao cabo AB. Observa-se que a esfera processa a uma taxa constante ϕ ˙ = 6 r a d / s em torno do eixo vertical AD. Sabendo que β = 40 ∘ , de
Um cubo sólido do lado c = 80 mm é preso como mostrado ao cabo AB. Observa-se que gira a uma taxa ψ ˙ = 40 r a d / s em torno de sua diagonal BC e precessa a uma taxa constante ϕ ˙ = 5 r a d / s em to