Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 140

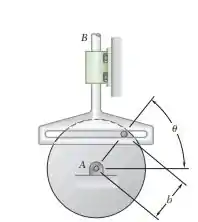
15.140. O disco de acionamento do mecanismo de cruzeta escocesa mostrado na figura tem uma velocidade angular ω e uma aceleração angular α , ambas no sentido anti-horário. Usando o método da Seção 15.9, deduza expressões para a velocidade e a aceleração do ponto B.

Passo 1

Vamos começar mais uma! De acordo com o método da seção 15.9 temos:

y B = l + y P

No caso da imagem

y B = l + b sin ⁡ θ

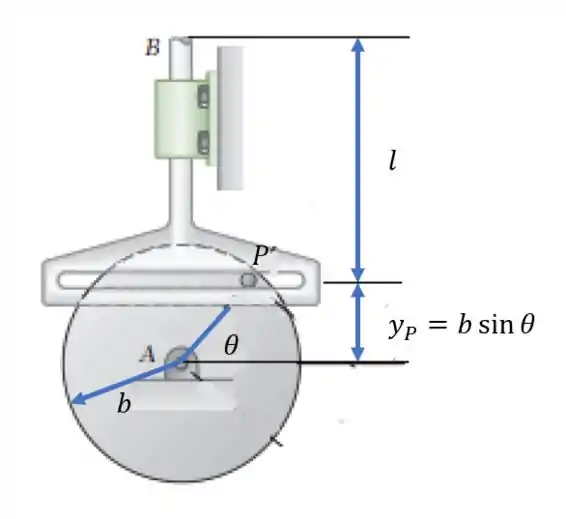
Passo 2

Temos também que

v B = y ˙ B

E

y ˙ B = d d t l + b sin ⁡ θ

Isso fica

y ˙ B = 0 + b cos ⁡ θ ⋅ θ ˙ = b cos ⁡ θ ⋅ ω

Então

v B = b cos ⁡ θ ⋅ ω

Deduzimos a velocidade, agora só falta a aceleração.

Passo 3

Também temos

a B = y ¨ B

E

y ¨ B = d d t y ˙ B

Logo

y ¨ B = d d t b cos ⁡ θ ⋅ ω

Isso fica

y ¨ B = - b sin ⁡ θ ⋅ θ ˙ 2 + b cos ⁡ θ ⋅ θ ¨

Logo

a B = b cos ⁡ θ ⋅ α - b sin ⁡ θ ⋅ ω 2

Resposta

v B = b cos ⁡ θ ⋅ ω

a B = b cos ⁡ θ ⋅ α - b sin ⁡ θ ⋅ ω 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No instante mostrado, o carro A se desloca com uma velocidade de 25 m/s, que está aumentando a uma taxa constante de 2 m/s², enquanto o carro C se desloca com uma velocidade de 15 m/s, que está aument
No instante mostrado, o barco A se desloca com uma velocidade de 15 m/s, que está diminuindo a 3 m/s², enquanto o barco B se desloca com uma velocidade de 10 m/s, que está aumentando a 2 m/s². Determi
No instante mostrado, o carro B se desloca com uma velocidade de 15 m/s, que está aumentando a uma taxa constante de 2 m/s², enquanto o carro C se desloca com uma velocidade de 15 m/s, que está aument
Uma estação de radar B situada no equador observa um satélite A em uma órbita circular equatorial de 200 km de altitude e se movendo de oeste para leste. Para o instante em que o satélite está 30 ° ac
A roda rola sobre a superfície circular sem deslizar. Na posição mais baixa, possui uma velocidade angular ω e uma aceleração angular α , ambas no sentido horário. Para essa posição, obtenha expressõe