Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.4 - Ex. 62
O disco semicircular de massa e raio é liberado a partir do repouso em e gira livremente no plano vertical em relação ao seu mancal fixo em . Desenvolva expressões para as componentes e da força sobre o mancal como funções de .
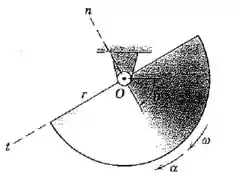
Passo 1
Vamos começar escrevendo as expressões para as forças, e então saberemos o que precisamos calcular.
Na direção temos o seguinte:
Onde é a componente normal da força sobre o mancal.
E na direção :
Onde é a componente tangencial da força sobre o mancal.
Então nosso problema é encontrar e em função de . Sabendo que a posição do centro de massa é .
Passo 2
Vamos começar encontrando , vamos usar a seguinte equação:
E a única força externa produzindo momento em torno do ponto é o peso do disco:
E o momento de inércia de um disco semicircular em relação ao seu centro é:
Então:
E com isso já podemos escrever a força :
Passo 3
E agora precisamos encontrar , podemos aproveitar para isso, basta lembrar da seguinte relação:
E agora vamos substituir e integrar:
E com isso já podemos escrever :
Resposta
As forças são e .