Enunciado
Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.2 - Ex. 9
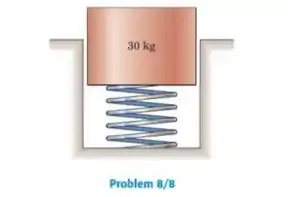
Para o cilindro do Prob. 8/8, determine o deslocamento vertical x, medido para baixo no sentido positivo em milímetros, a partir da posição de equilibro, em termos do tempo t, em segundos, medido a partir do instante de liberação da posição de 25mm de deflexão adicional.
Passo 1
Bom, primeiro vamos escrever a equação do movimento oscilatório:
Vamos determinar primeiro as duas constantes que acompanham as funções seno e cosseno, para isso precisaremos da derivada de x, pois trata-se de duas incógnitas então precisamos de duas equações.
E a sua derivada será:
Passo 2
Para :
Pois a velocidade inicial é igual a zero
Nossa equação de movimento então será:
Passo 3
Como o cilindro foi abaixado 0.25m, . E a frequência natural pode ser calculada utilizando a frequência em ciclos por segundo do resultado do problema 8/8:
A equação fica: