Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 77
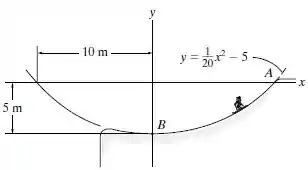
Uma esquiadora parte do repouso em (10m, 0) e desce o declive liso que pode ser aproximado por uma parábola. Se a esquiadora tem massa de 52 kg, determine a força normal que o solo exerce sobre ela no instante que ela chega ao ponto . Despreze a dimensão da esquiadora. Dica: use o resultado do Problema 13.75.
Passo 1
Sabemos que o declive é liso, portanto a Força de Resistência à tração é desprezível (, e que ele é definido pela seguinte equação:
Além disso, temos os seguintes dados:
massa da esquiadora: kg
gravidade: m/s2
Coordenadas ponto : (10m, 0)
Coordenadas ponto : (0, - 5m)
Velocidade incial m/s
Analisando o enunciado, podemos ver que o problema envolve o movimento do corpo ao longo de uma trajetória curva conhecida. Quando temos este tipo de trajetória, é necessário traçar um novo eixo com as coordenadas normais e tangenciais a fim de facilitar a resolução do problema. Assim, obtemos o seguinte diagrama de corpo livre:
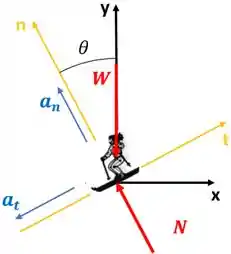
Onde = força peso
= força normal resultante
= aceleração tangencial
=aceleração normal
Sabemos que
Onde é o raio de curvatura no ponto onde o corpo está localizado.
A questão pede para encontrarmos a Força Normal no ponto (0, -5m).
Passo 2
Primeiramente, analisamos a geometria da situação. Temos que
Para o ponto , m, temos
Em seguida, devemos encontrar o ângulo no ponto .
Olhando novamente o diagrama de corpo livre, podemos ver que
Logo, para m, temos
Passo 3
Agora, com os dados obtidos, utilizaremos as Equações de Movimento.
Aplicando a Equação do Movimento no sentindo do eixo , temos
Aplicando a Equação do Movimento no sentido do eixo , temos
Passo 4
Prara definirmos o valor de , precisamos encontrar o valor de .
O enunciado nos dá a dica para usarmos o resultado da questão 13.75. Nela temos que , independente da trajetória.
Portanto, o valor de será
Passo 5
Substituindo m/s2, e m em
Teremos,