Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 17.Problemas - Ex. 14

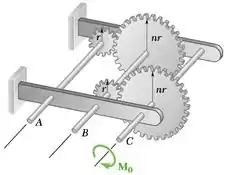
O trem de engrenagens mostrado na figura consiste de quatro engrenagens de mesma espessura e do mesmo material: duas engrenagens têm raio r e as outras duas tem raio nr. O sistema está em repouso quando o binário M0 é aplicado no eixo C. Indicado por I0 o momento de inércia de uma engrenagem de raio r, determine a velocidade angular do eixo A se o binário M0 é aplicado para uma revolução do eixo C.

Passo 1

O enunciado pede que a gente determine a velocidade angular do eixo A se o binário M0 é aplicado para uma revolução do eixo C.

Massa e momento de inércia.

Para um disco de raio r e espessura t:

m = ρ π r 2 t = ρ π t r 2

I - 0 = 1 2 m r 2 = 1 2 ρ π + r 2 r 2 = 1 2 ρ π t r 4

Passo 2

Para um disco de raio nr e espessura t:

I - = 1 2 ρ π t n r 4                 I - = n 4 I - 0

Cinemática:

Se para o eixo A, temos ω A  

Então, para o eixo B, temos ω B = ω A / n  

E, para o eixo B, temos ω C = ω A / n 2  

Princípio da energia de trabalho:

Acople M0 aplicado ao eixo C para uma revolução, θ = 2 π radianos, T1 = 0,

U 1 → 2 = M 0 θ = M 0 2 π   radianos = 2 π M 0

T 2 = 1 2 I - eixo  A w A 2 + 1 2 I - eixo  B ω B 2 + 1 2 I - eixo  C ω C 2 = 1 2 I - 0 ω A 2 + 1 2 I - 0 + n 4 I - 0 ω A n 2 + 1 2 n 4 I - 0 ω A n 2 2 = 1 2 I - 0 ω A 2 n 2 + 2 + 1 n 2

= 1 2 I - 0 ω A 2 n + 1 n 2

Passo 3

T 1 + U 1 - 2 = T 2 :                 0 + 2 π M 0 = 1 2 I - 0 ω A 2 n + 1 n 2

Velocidade angular.

ω A 2 = 4 π M 0 I - 0 1 n + 1 n 2

Resposta

ω A = 2 n n 2 + 1 π M 0 I - 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma moeda é lançada ao ar. Observa-se girar a uma taxa de 600 rpm em torno de um eixo GC perpendicular à moeda e processar em torno da direção vertical GD. Sabendo que GC forma um ângulo de 15° com GD
Um cubo sólido do lado c = 120 mm é preso como mostrado a um cabo AB de comprimento 240 mm. O cubo gira em torno de sua diagonal BC e processa em torno do eixo vertical AD. Sabendo que θ = 25 ∘ e β =
Um registro fotográfico de alta velocidade mostra que um determinado projétil foi disparado com uma velocidade horizontal V de 600 m / se com seu eixo de simetria formando um ângulo β = 3 ∘ com a hori
Uma placa retangular homogênea de massa nos lados c e 2c é mantida em A e B por um eixo com extremidade em garfo de massa desprezível, que é suportado por um rolamento em C. A placa está livre para gi
Considere um corpo rígido de forma arbitrária, que é fixado em seu centro de massa 0 e submetido a nenhuma força além de seu peso e a reação do suporte em 0. (a) Prove que o momento angular H O do cor