Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 41

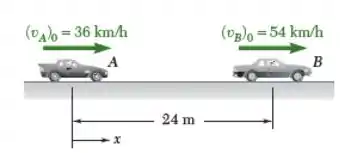
Dois automóveis A e B viajam no mesmo sentido em pistas adjacentes e, em t = 0 , têm suas posições e velocidades escalares mostradas na fiura. Sabendo que o automóvel A tem uma aceleração constante de 0,5 m / s ² e que B tem uma desaceleração de 0,3 m / s ² , determine (a) quando e onde A vai ultrapassar B, (b) a velocidade de cada automóvel naquele instante.

Passo 1

a A = + 1,8 f t / s ² a B = - 1,2 f t / s ²

v A 0 = 24 m i / h = 35,2 f t / s

v B 0 = 36 m i / h = 52,8 f t / s

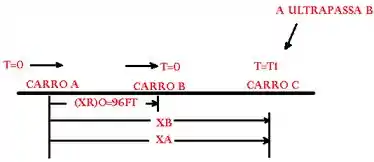
Movimento do automóvel A:

v A = v A 0 + a A t = 35,2 + 1,8 t x A = x A 0 + ( v A ) 0 t + 1 2 a A t ² = 0 + 35,2 t + 1 2   x   ( 1,8 ) t ²

Movimento do automóvel B:

v B = v B 0 + a B t = 52,8 - 1,2 t x B = x B 0 + ( v B ) 0 t + 1 2 a B t ² = 75 + 52,8 t + 1 2   x   ( - 1,2 ) t ²

Passo 2

  1. A ultrapassa B em t = t 1 .

    2. x A = x B : 35,2 t + 0,9 t 1 2 = 75 + 52,8 t 1 - 0,6 t 1 2 1,5 t 1 2 - 17,6 t 1 - 75 = 0 t 1 = - 3,22 s e t 1 = 15,0546

    Eq.(2): x A = 35,2   x   15,05 + 0,9   x   ( 15,05 ) ²

  2. Velocidades quando: t 1 = 15,05 s

Eq.(1): v A = 35,2 + 1,8   x   15,05

v A = 62,29 f t / s

Eq.(3): v B = 52,8 - 1,2   x   15,05

v B = 34,74 f t / s

Resposta

  1. t 1 = 15,05 s

    2. Eq. (2): x A = 734 f t

  2. Eq.(1): v A = 42,5 m i / h →

Eq.(3): v B = 23,7 m i / h →

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O carro A parte do repouso em t = 0 e move-se ao longo de uma estrada reta com uma aceleração constante de 2m / s 2 até alcançar uma velocidade de 27m / s . Depois disso, ele mantém essa velocidade. Q
Uma partícula move-se ao longo de uma linha reta com uma velocidade v = 12 - 3 t 2m / s , onde t é dado em segundos. Quando t = 1s , a partícula está localizada 10m à esquerda da origem. Determine a a
Uma partícula move-se ao longo de uma trajetória em linha reta de tal maneira que em 4 s ela se move de uma posição inicial s a = - 8m para uma posição s b = + 3m . Então, em mais 5 s, ela move-se de
Uma partícula move-se ao longo de uma linha reta de tal maneira que em 2s ela se move de uma posição inicial s a = + 0,5m para uma posição s b = - 1,5m . Então, em mais 4s , ela move-se de s b para s
Testes revelam que um motorista normal leva em torno de 0,75 s antes de poder reagir a uma situação para evitar uma colisão. Um motorista com 0,1% de álcool no seu sistema leva em torno de 3 s para fa