Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 8.Problemas - Ex. 51
O coeficiente de atrito estático entre as sapatas das pinças em A e B e o engradado é , e entre ele e o piso é . Se uma força de arrasto horizontal de é aplicada às pinças, determine a maior massa que pode ser arrastada.
Passo 1
Fala aí, galerinha do Responde aí. Tudo bem? Bora pra mais uma questão.
Primeiramente, vamos decompor as reações que surgem na união das barras com as correntes. Temos a seguinte situação:
Decompondo a força em componentes verticais e horizontais em cada corrente:
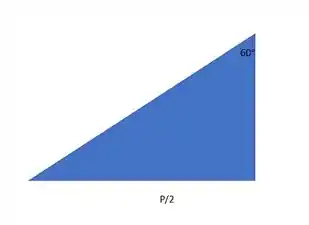
Sabemos que a componente horizontal nas correntes deve totalizar logo, teremos em cada corrente. Para achar a componente vertical, basta aplicar:
Passo 2
Agora, vamos usar um pouco de malandragem. Essas componentes verticais são transmitidas até o apoio nos pontos e Ou seja, a força normal (que precisamos para achar o atrito) nos pontos é igual a:
Logo, a força de atrito no apoio vale:
Passo 3
Por fim, a força de atrito entre o bloco e o chão deve ser menor que a força de atrito do apoio, ou o apoio irá romper. Logo:
Igualando as forças:
Essa é a maior massa que pode ser arrastada.