Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 46

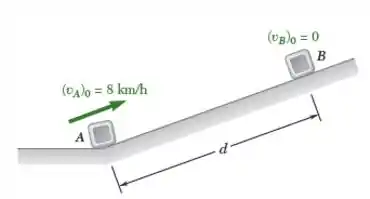
Dois blocos A e B são colocados em uma inclinação como mostrado na figura. Em t = 0 ,   A é projetado para cima na inclinação com uma velocidade inicial de 8 m / s e B é liberado em repouso. Os blocos passam um pelo outro após 1 s e B alcança a base da inclinação quando t = 3,4 s . Sabendo que a distancia máxima alcançada pelo bloco A a partir da base da inclinação é 6 m e a aceleração de A e B (devido à gravidade e ao atrito) são constantes e direcionadas para baixo na inclinação, determine (a) a aceleração de A e B, (b) a distancia de d, (c) a velocidade escalar de A quando os blocos passam um pelo outro.

Passo 1

  1. Temos: v A 2 = ( v A ) 0 2 + 2 a A   x   [ x A - 0 ]

    2. Quando x A = ( x A ) m a x ,       v A = 0

    Então: 0 = ( 27 f t / s ) ² + 2 a A   x   ( 21 f t )

    Ou a A = - 17,357 f t / s ²

    Agora x A = 0 + ( v A ) 0 t + 1 2 a A t ²

    E x B = 0 + 0 t + 1 2 a B t ²

    Em t = 1 s , os blocos se cruzam.

    ( x A ) 1 + ( x B ) 1 = d

    Em t = 3,4 s ,     x B = d :

    Portanto x A 1 + x B 1 = x B 3.4

    Ou [ ( 27 f t / s )   x   ( 1 s ) + 1 2   x   ( - 17,3571 f t / s ² )   x   ( 1 s ) ² ]  

    + 1 2 a B   x   1 s 2 = 1 2 a B   x   3,4 2 a B = 3,4700 f t / s ²

    Passo 2

  2. Em t = 3,4 s ,       x B = d : d = 1 2   x   ( 3,4700 f t / s ² )   x   ( 3,4 s ) ²
  3. Temos: v A = ( v A ) 0 + a A t

Em t = 1 s : v A = 27 f t / s + ( - 17,3571 f t / s )   x   ( 1 s )

Resposta

  1. a A = 17,36 f t / s ² ↓

    2. a B = 3,47 f t / s ² ↓

  2. d = 20,1 f t
  3. v A = 9,64 f t / s
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Conforme um trem acelera uniformemente, ele passa por sucessivas marcas de um quilômetro enquanto se move a velocidades de 2 m/s e, em seguida, 10 m/s. Determine a velocidade do trem quando ele passar
Um carro parte do repouso e move-se com uma aceleração constante de 1,5 m/s2 até alcançar uma velocidade de 25 m/s. Em seguida, move-se com uma velocidade constante por 60 segundos. Determine a veloci
Uma partícula parte do repouso e move-se ao longo de uma linha reta com uma aceleração a = 30 - 0,2 vm / s 2 , onde v é dado em m/s. Determine o tempo quando a velocidade da partícula for v = 30m / s
Uma esfera é atirada para baixo em um meio com uma velocidade inicial de 27 m/s. Se ela experimenta uma desaceleração de a = - 6 tm / s 2 , onde t é dado em segundos, determine a distância percorrida
Uma partícula está se movendo ao longo de uma linha reta de maneira que sua velocidade é definida como v = - 4 s 2m / s , onde s é dado em metros. Se s=2 m quando t=0, determine a velocidade e a acele