Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 161
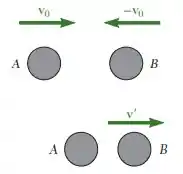
Dois discos deslizam sobre um plano horizontal sem atrito com velocidades de sentidos opostos e de mesma intensidade e batem de frente. Sabe-se que o disco tem uma massa de e observa-se que ele tem velocidade nula após o impacto. Determine a massa do disco , sabendo que o coeficiente de restituição entre os dois discos é e a faixa de valores possíveis da massa de se o coeficiente de restituição entre os dois discos é desconhecido.
Passo 1
Fala aí, galera. Beleza? Bora fazer mais um exercício. Primeiro, temos que determinar a massa do disco quando o coeficiente de restituição é . Para isso, vamos começar utilizando a equação de conservação de momento linear, dada por:
Sabemos que e que a , vamos substituir:
Isolando :
Em seguida, vamos utilizar a relação entre as velocidades iniciais e finais e o coeficiente de restituição a fim de encontrarmos uma segunda equação. Temos:
Substituindo:
Opa, galera temos um sistema linear de duas equações e duas incógnitas. Para resolver este sisteminha, vamos substituir a equação na equação . Fica assim:
Opa, encontramos a massa do disco .
Passo 2
Em seguida, vamos para a segunda parte do problema. Nela, temos que encontrar a faixa de valores possíveis da massa de se o coeficiente de restituição entre os dois discos é desconhecido.
Para isso, vamos utilizar as mesmas relações que utilizamos no passo anterior. Pela conservação de momento linear sabemos que:
E então, vamos utilizar a relação entre as velocidades iniciais e finais e o coeficiente de restituição a fim de encontrarmos uma segunda equação. Temos:
Desta vez é desconhecido, portanto:
Com isso, para encontrarmos a faixa pedida, temos que resolver o sistema linear. Para isso, temos que substituir a equação na equação . Fica assim:
Assim, a faixa vai ser:
Isso é tudo, pessoal! Bora fazer mais questões para ficar craque.