Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 19.Problemas - Ex. 111
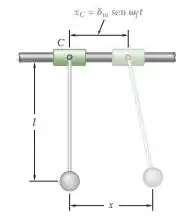
19.111. Um pêndulo simples de comprimento l é suspenso de um cursor C que é forçado a mover-se horizontalmente de acordo com a relação . Determine o intervalo de valores de f para o qual o movimento do peso seja menor que m. (Considere que m é pequeno comparado com o comprimento l do pêndulo.)
Passo 1
Vamos começar essa questão aqui fazendo uma equação para , que é a função posição da massa que está pendurada.
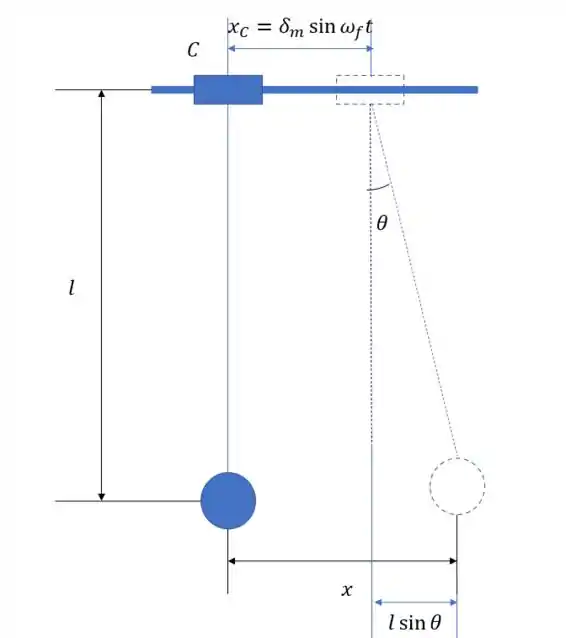
Olha só, na imagem a gente pode ver que
Isso é a mesma coisa que dizer que
Passo 2
Agora vamos fazer o diagrama de forças
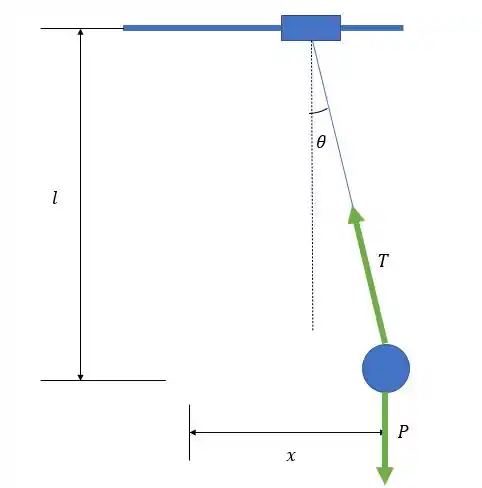
A gente pode fazer uma malandragem no eixo vertical, olha só, como estamos falando de ângulos pequenos nesse problema, podemos dizer que o deslocamento no eixo é aproximadamente 0.
Isso traz algumas consequências interessantes para a gente, como aproximamos para um sistema onde não tem movimento no eixo , significa que a aceleração no eixo também é aproximadamente nula.
Agora com a segunda lei de Newton podemos fazer
Logo
E isso leva a uma consequência interessante para a gente
Em que
Só nos resta trabalhar com o eixo , que é o ponto chave da questão.
Com a segunda lei de Newton temos
Então a equação de movimento fica
E agora tudo vai começar a se encaixar, porque já tínhamos calculado um valor para
Então
Agora vamos substituir o valor de
A gente pode melhorar um pouquinho essa equação, primeiro vamos cortar
Agora vamos distribuir
Passo 3
Vamos pegar essa equação que a gente desenvolveu agora, e substituir o valor de que o enunciado nos dá
Agora as coisas vão começar a ficar interessantes, porque nós temos uma equação para a frequência natural
Isso é o mesmo que dizer
Agora vamos substituir isso na equação
Beleza, a gente já está chegando em algum lugar. A gente pode calcular a amplitude da vibração assim:
Isso é o mesmo que dizer que
E matematicamente, sabemos que
Claro, estamos considerando que
Então
Vamos considerar aqui que
Passo 4
Beleza, agora vamos focar na parte da expressão
Isso aqui é obrigatoriamente maior ou igual a , já que sabemos
Então
Aqui podemos já de imediato ver que existem dois valores para que a equação seja
Ou
Então, para ser valido a inequação
Os valores não podem estar no intervalo
Ou
Pois vamos pegar apenas os valores positivos, então não pode ser menor que zero.
Logo
Então