Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 67
O eixo tem raio e está sujeito a um torque por unidade de comprimento distribuído uniformemente por todo o comprimento do eixo. Se ele estiver preso em sua extremidade distante , determine o ângulo de torção na extremidade . O módulo de cisalhamento é .
Passo 1
Olá, pessoal! Tudo bem? Vamos analisar essa questão?
O passo que julgo mais difícil é determinar qual é o torque que produz essa torção. Para isso faremos um corte no eixo:
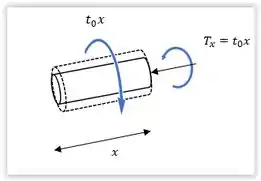
Como o torque é uniformemente distribuído por uma unidade de comprimento podemos analisar que o torque produzido é igual à carga de torque multiplicada pelo comprimento .
Passo 2
Agora com o torque determinado, iremos utilizar a definição de ângulo de deformação descrito pela equação:
Como não ocorre a variação de diâmetro no eixo e o seu material é homogêneo podemos tirar as constantes e da equação, o que resulta na equação:
A carga de toque é uma constante também, com isso nos resta apenas calcular a integral de :
Como a secção é circular e maciça, temos que;
Substituindo na equação: