Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 68
O parafuso de aço A-36 é apertado dentro de um furo de modo que o torque de reação na haste pode ser expresso pela equação, onde é dado em metros. Se um torque for aplicado à cabeça do parafuso, determine a constante e a quantidade de torção nos de comprimento da haste. Considere que a haste tem um raio constante de .
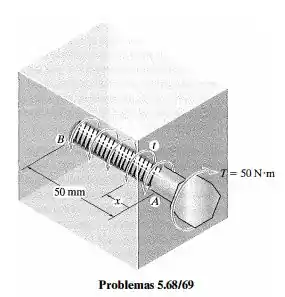
Passo 1
Olá, pessoal! Vamos lá analisar esse problema?
O enunciado pede o ângulo de torção na haste e, para isso, teremos de descobrir a constante para calcular o valor do carregamento de reação.
Vamos então anotar os dados que temos:
Aço A-36, portanto,
Só com os dados iniciais é possível calcular o momento polar de inércia da seção circular da haste:
Passo 2
Primeiro, temos que descobrir a constante , e para isso vamos usar um trecho muito importante do enunciado: “O parafuso de aço A-36 é apertado dentro de um furo de modo que o torque de reação na haste pode ser expresso pela equação ”.
Com isso podemos igualar os torques no parafuso: o torque produzido pelo carregamento, , com o torque aplicado na cabeça do parafuso.
Temos que é o toque total produzido pelo carregamento, o somatório dos torques em cada mínimo comprimento (), ou seja,
Com o valor da constante encontrado, temos que o valor do torque produzido pelo carregamento a um comprimento é:
O torque que provocara o ângulo de torção é dado pelo torque da cabeça do parafuso menos o torque do carregamento, pois como podemos observar na figura a seguir, eles estão em sentidos opostos.
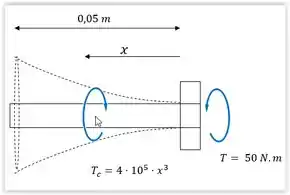
Com isso temos que:
Passo 3
Agora nos resta calcular o ângulo de torção :
Convertendo para radianos: