Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.8 - Ex. 189

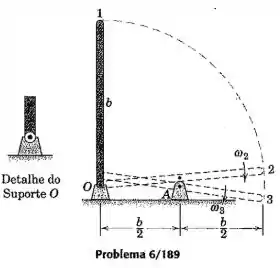
A barra esbelta de massa m e comprimento b é articulada na sua extremidade inferior em O , na forma mostrada no detalhe separado do suporte O . A barra é liberada a partir do repouso na posição vertical 1. Quando o ponto médio da barra atinge a articulação em A na posição 2, torna-se preso à articulação, e simultaneamente a articulação em O se desacopla. Determine a velocidade angular ω 3 da barra logo após se acoplar na articulação em A na posição 3.

Passo 1

Na ausência de forças extermas e forças elásticas, da posição 1 para a posição 2, temos

∆ T + ∆ V g = 0

De onde tiramos que

1 2 I o ω 2 2 - 0 + 0 - m g b 2 = 0  

Mas, lembrando o tópico de momento de inércia de massa, sabemos que, para a barra esbelta

I o = 1 3 m b ²

Daí, obtemos

1 3 m b 2 ω 2 2 = m g b 2

Resolvendo para ω 2 , encontramos

ω 2 = 3 g b   2

Passo 2

Durante a colisão da barra esbelta com a articulação em A (posição 2 → 3 ), a quantidade de movimento angular é conservada, de forma que

H A 2 = H A 2

I - ω 2 = I - ω 3                 ∴                     ω 2 = ω 3 = 3 g b   2

Resposta

ω 3 = 3 g b   2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um cursor de 5 kg pode deslizar sobre uma barra horizontal sem atritoe está ligado a uma mola de constante k. Sobre ele atua uma força periódica de intensidade P = P ms e nω ƒ t ƒ , onde P m = 10N e ω
Um bloco A de 8 kg desliza em uma fenda vertical sem atrito e está ligado a um suporte móvel B por meio de uma mola de constante k = 120 N/m. Sabendo que a aceleração do suporte é a = a ms e nω ƒ t ,o
Um disco uniforme de 8 kg e raio de 200 mm é soldado a um eixo vertical com uma ponta engastada em B. O disco gira em um ângulo de 3° quando um binário estático de intensidade de 50N ∙ m lhe é aplicad
A barra AB é rigidamente presa à estrutura de um motor em funcionamento com velocidade constante. Quando um cursor de massa m é colocado sobre a mola, observa-se que ele tem amplitude de 15 mm. Quando
As Figuras (1) e (2) mostram como molas podem ser usadas para suportar um bloco em duas situações diferentes. Na Fig. (1), elas ajudam a diminuir a amplitude da força oscilante transmitida pelo blocoà