Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 92

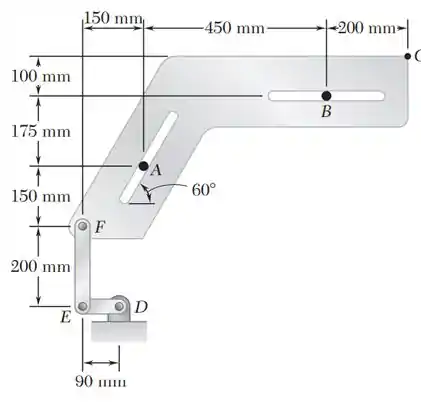
Dois rasgos foram abertos na placa F G e a placa foi posicionada de tal forma que os rasgos são ajustados a dois pinos fixos A e B . Sabendo que no instante mostrado na figura a velocidade angular da manivela D E é de 6   r a d   / s no sentido horário, determine (a) a velocidade do ponto F , (b) a velocidade do ponto G .

Passo 1

Bora pra questão 92 agora, meus caros(as)!

E já sabe, né! Nada melhor do que uma figura pra ajudar a entender uma questão.

Vamos faze um esboço destacando vetorialmente as velocidades e o centro de rotação instantâneo desse sistema.

Aqui está, nosso belo esboço... Não ficou uma beleza!?

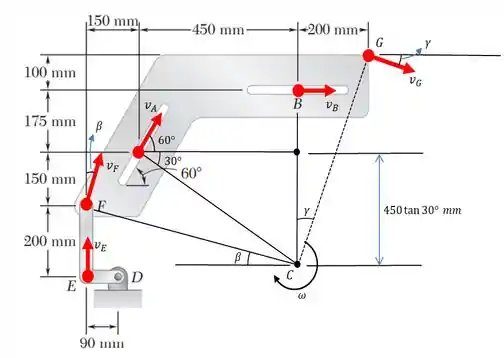
Passo 2

a) Bom! Inicialmente, a gente tem que determinar a velocidade do ponto F , que chamamos de v F !

Pois muito bem! Comecemos calculando v E , que pela figura, podemos ver que é dada por...

v E = D E ω D E

E como a velocidade angular da manivela D E é de 6   r a d   / s no sentido horário, então...

v E = 90   m m ( 6   r a d / s )

v E = 540   m m / s   ↑

Essa velocidade v E vai ser a velocidade em E e também vai estar agindo na barra E F . Se você ai não entendeu, se liga na imagem abaixo, que mostra o diagrama de velocidades na barra E F ...

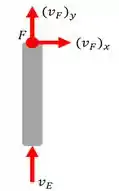
Baseado nisso, a gente tem que...

v F y = v E = 540   m m / s   ↑

Olhando então, a figura do P a s s o   2 , temos que...

v F = C F ω

Agora se liga! Decompondo esse v f em   y , obtemos que

v F y = C F ω cos ⁡ β

v F y = C F cos ⁡ β ω

Só que...

C F cos ⁡ β = 600   m m

Logo, podemos obter o valor da velocidade angular da placa isolando ω :

ω = v F y C F cos ⁡ β

ω = 540   m m / s 600   m m

ω = 0,9   r a d / s   ⤾

Que assim como a da manivela, também está no sentido horário!

Passo 3

Agora é a vez de obter o valor de A C ...

Se liga! Dá pra fazer isso pelo Teorema de Pitágoras! Olhando a figura do P a s s o   1 , temos que...

C F 2 = 600   m m 2 + 450 tan ⁡ 30 ° - 150   m m 2

C F 2 = 372057,71   m m 2

C F = 609,96   m m

E então, podemos obter β :

C F cos ⁡ β = 600   m m

609,96   m m cos ⁡ β = 600   m m

cos ⁡ β = 600   m m 609,96   m m

β = cos - 1 ⁡ 600   m m 609,96   m m

β = 10,37 °

Que beleza! v F assim, será igual à...

v F = C F ω

v F = 609,96   m m ( 0,9   r a d / s )

v F = 548,96   m m / s

Escrevendo em módulo e ângulo...

v F = 548,96   m m / s   ⦬   10,37 °

Pronto! A primeira parte da missão já foi cumprida!

Passo 4

b) Vamos agora pra segunda parte! E aqui, temos que obter v G !

Pela figura do P a s s o   2 , podemos ver que ele é dado por...

v G = C G ω

Vamos então tratar de obter C G . Olhando a imagem, nós temos que

tan ⁡ γ = 200   m m 450 tan ⁡ 30 °   m m + 175   m m + 100   m m

γ = tan - 1 ⁡ 200   m m 450 tan ⁡ 30 °   m m + 175   m m + 100   m m

γ = tan - 1 ⁡ 0,3739

γ = 20,504 °

Sendo assim, obtido γ ... Para achar C G basta utilizar a relação seno...

sen ⁡ γ = 200   m m C G

C G = 200   m m sen ⁡ γ

C G = 200   m m sen ⁡ 20,504 °

C G = 570,98   m m

Aí sim, meus colegas! Demorou mais chegou! Já podemos obter o valor de v G :

v G = C G ω

v G = 570,98   m m ( 0,9   r a d / s )

v G = 513,88   m m / s ≅ 514   m m / s

Sendo assim, em módulo e ângulo, chegamos ao seguinte resultado...

v G ≅ 514   m m / s   ⦪   20,504 °

Terminamos aqui! Até a próxima!

Resposta

a)

v F = 548,96   m m / s   ⦬   10,37 °

b)

v G ≅ 514   m m / s   ⦪   20,504 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O cilindro de 12 kg sustentado pelos suportes dos mancais em A e B tem um momento de inércia em relação ao eixo vertical z 0 por meio de seu centro de massa G igual a 0,080k g ∙ m 2 . O disco e os sup
Cada uma das duas barras esbeltas uniformes O A e B C possui uma massa de 8k g . As barras estão soldadas em A para formar um elemento com formato de T e estão girando livremente em torno de um eixo h
A haste B de 0,4k g com centro de massa a 55m m de O - O tem um raio de giração de 69m m em relação a O - O . A haste está soldada ao tubo de aço e é livre para girar em torno do eixo horizontal fixo
Um cabo flexível com 60 metros de comprimento, com uma massa de 0,160k g por metro de comprimento, está enrolado em volta do tambor. Com y = 0 , o peso do cilindro de 4k g é necessário para iniciar a
Em 1993 , o ônibus espacial capturou o telescópio Hubble em órbita e fixou-o ao compartimento de carga para reparos, na configuração simulada na figura. Durante o período de reparo era importante limi