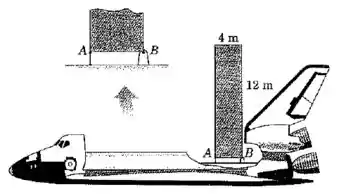
Em , o ônibus espacial capturou o telescópio Hubble em órbita e fixou-o ao compartimento de carga para reparos, na configuração simulada na figura. Durante o período de reparo era importante limitar qualquer aceleração angular do ônibus espacial de modo a não induzir forças excessivas nas travas que prendiam o telescópio ao ônibus. Para ilustrar a dinâmica envolvida, substitua o telescópio por uma placa plana homogênea de presa na forma simplificada indicada na vista explodida. Calcule a acelreação angular máxima no sentido anti-horário que o ônibus espacial pode ter, de modo a não exceder uma tração de no elemento de ligação em . Para essa condição, calcule também a força correspondente suportada pelo pino em . Faça seus cálculos em relação a um sistema de referência sem rotação que se desloca com o ônibus espacial em sua órbita.
Passo 1
Vamos começar representando as forças que agem sobre a placa homogênea:
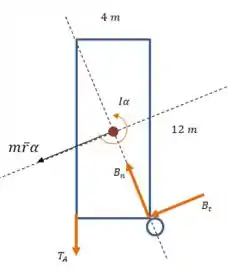
Onde consideramos que, por estar em órbita, a placa não tem peso no referencial do ônibus espacial.
Passo 2
Agora vamos calcular o momento resultante em relação ao ponto , com a intenção de encontrar a aceleração angular no caso limite em que .
A única força que produz momento em relação ao ponto é , que está a uma distância perpendicular de :
E podemos calcular a distância entre o centro de massa e o ponto usando o teorema de pitágoras:
E então:
E o momento de inércia da chapa retangular é:
Então:
Passo 3
Agora que conhecemos a aceleração angular, podemos aplicar a segunda lei de Newton para encontrar as forças e .
Começamos analisando a direção normal, onde a força resultante é nula:
Onde é um ângulo que vamos definir em breve.
E na direção tangencial:
Então as componentes são:
Onde é o seguinte ângulo:
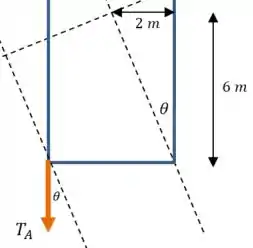
Agora vamos substituir isso, e os outros valore numéricos, nas nossas expressões para as forças em .
Começando pela tangencial:
E a componente normal é:
De forma que o módulo total da força é:
Resposta
A força total suportada em é de , e a aceleração angular máxima é .