Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 5.Problemas - Ex. 35
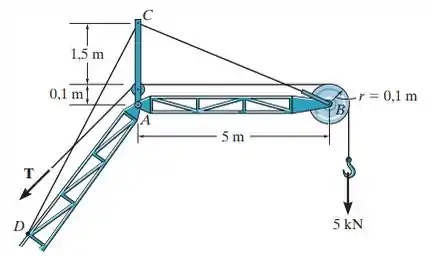
A parte superior do guindaste consiste na lança , que é apoiada pelo pino em , o cabo de sustentação e o cabo , cada cabo sendo preso separadamente ao mastro em . Se a carga de 5 kN for apoiada pelo cabo de levantamento, que passa pela polia em , determine a intensidade da força resultante que o pino exerce sobre a lança em para que haja equilíbrio, a tração no cabo de sustentação e a tração no cabo de levantamento. Desconsidere o peso da lança. A polia em tem um raio de 0,1 m.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Esta é uma questão um pouco confusa por causa da geometria, mas não é algo impossível. Na realidade, ela vai fluir tranquilamente.
A questão pede para calcularmos a força resultante do pino em , a tração no cabo de sustentação e a tração no cabo.
Dentre estes três parâmetros, o mais fácil de determinar é a tração no cabo! Dizemos isto pois ela é exatamente o valor do peso que o guindaste carrega! Logo,
E assim temos a nossa primeira reação!
Passo 2
Só nos resta agora determinarmos as reações e , no cabo de tração e pino respectivamente.
Do nosso sistema, apenas a reação possui componente vertical para equilibrar com os para baixo do peso! Portanto, avaliando o equilíbrio das forças na direção , temos:
E assim descobrimos a segunda incógnita! Para finalizarmos a questão, basta calcularmos o somatório de forças na direção ! Aqui é importante lembrarmos que a força de também está nesta direção, isto devido ao cabo. Portanto,
E assim finalizamos a questão!