Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas de Revisão - Ex. 126

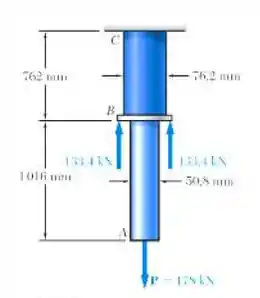
Duas barras cilíndricas solidam são unidas em B e carregada conforme mostra a figura. A barra é feita de aço ( E = 200   G P a ) e a barra BC, de latão ( E = 103,4   G P a ) . Determine (a) o deslocamento total da barra composta ABC e (b) o deslocamento do ponto B.

Passo 1

E ai gurizada tudo belezinha? O enunciado pede que a gente determine o deslocamento total da barra composta ABC e o deslocamento do ponto B.

Vamos trazer os dados da parte AB:

P A B = 178   x   10 3   N L A B = 1,016   m d = 0,0508   m A A B = π 4 d 2 = π 4   x   0,0508   2 = 0,002026834656   m ² E A B = 200   x   10 6   P a

Agora podemos determinar o deslocamento :D δ A B = P A B L A B E A B A A B = 178   x   10 3   x   ( 1,016 ) 200   x   10 6   x   ( 0,002026834656 ) = 446,13   x   10 - 3   m

Passo 2

Na seção BC será similar ao passo 1:

P B C = - 133,4   x   10 3   P a L B C = 0,762   m d = 0,0762   m

Partiu determinar a área :D

A B C = π 4 d 2 = π 4   x   0,0762   2 = 4,56   x   10 - 3   m 2

Sabendo que E B C = 1 03,4   x   10 9   P a δ B C = P B C L B C E B C A B C = - 133,4   x   10 3     x   ( 0,762 ) 103,4   x   10 9   x   ( 4,56   x   10 - 3 ) = - 0,14373   m

  1. δ = δ A B + δ B C = 446,13   x   10 - 3 - 0,14373 =   0,3024 m
  2. δ B = - δ B C

Resposta

  1. δ = 0,3024   m ↓  
  2. - 0,14373   m ↑
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a viga prismática mostrada, determine a deflexão em A .
Para a viga e o carregamento mostrados, determine a deflexão do ponto B . Use E = 200G P a .
Para a viga e o carregamento mostrados, determine a deflexão do ponto D . Use E = 200G P a .
Para a treliça e o carregamento mostrados, determine a deflexão vertical e horizontal do nó C .
Para a viga e o carregamento mostrados, determine a deflexão do ponto B . Use E = 200G P a .