Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.8 - Ex. 97
As duas esferas estão presas à haste leve rígida, que está suspensa por um cordão a partir do suporte acima dela. Se as esferas e a haste, inicialmente em repouso, são atingidas com a força , calcule a aceleração correspondente do centro de massa e a taxa na qual a velocidade angular da barra está variando.
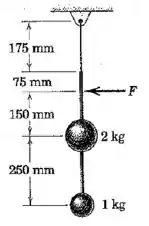
Passo 1
Podemos ser bem diretos para calcular a aceleração do centro de massa:
E como estamos aplicando essa equação na direção horizontal, não precisamos considerar os pesos das bolas e as forças de suporte.
E a massa total é:
E então a aceleração do centro de massa é:
Passo 2
Agora queremos calcular a aceleração angular da barra. Para isso vamos pensar em termos de momento angular.
É uma boa começar procurando a posição do centro de massa do sistema. Sabemos que vai estar em algum ponto entre as duas bolas:
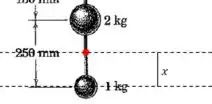
E então o momento angular total do sistema vai ser o seguinte:
Onde vai ser a distância de cada bola até o centro de massa:
Passo 3
Agora podemos lembrar do seguinte: a soma dos torques externos é necessariamente igual à taxa de variação do momento angular:
No nosso caso, o torque externo está associado à força :
E a derivada temporal de é:
E então:
Resposta
A aceleração do centro de massa , e a taxa de variação da velocidade angular é .