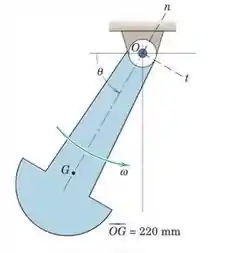
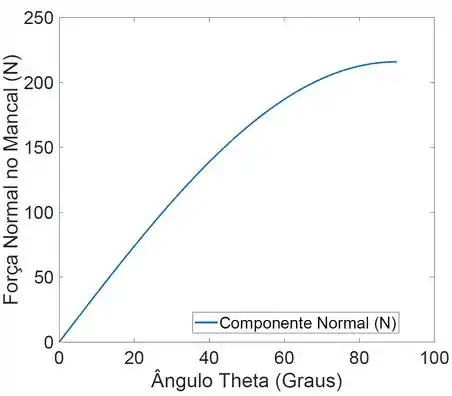
O pendulo de kg com centro de massa em e um raio de giração de mm em relação a é liberado a partir do repouso na posição horizontal .Represente graficamente a componete da força suportada pelo mancal em desde até . Indique o módulo máximo da componente da força no mancal .
Passo 1
Primeiramente é necessário determinar o DCL do corpo em analise, confomer a figura abaixo mostra.
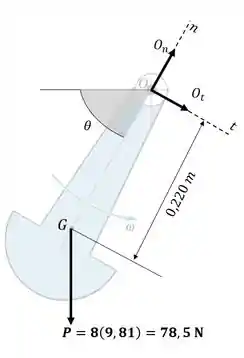
Também é necessário determinar o momento de inercia do pendulo para somatório de momentos
Passo 2
Realizando o somatório de momentos em relação afim de eliminar :
Para os somatório de forças
Para um dado ângulo , há quatro incógnitas nas três equações acima: . E não é constante; em vez disso, ela depende da posições da barra. A quarta equação necessária é obtida utilizando -se a cinemática, onde podem ser relacionados a pela equação:
Então,
Passo 3
Para o valor máximo do módulo de o valor de é zero
Utilizando a equação , foi plotado o comportamento da força normal em função do ângulo .
Resposta
O valor máximo da componente tangente é