Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 59

Duas forças de 4 kN são aplicadas ao elemento de máquina AB, como mostrado. Determinar as tensões, normal e de cisalhamento, no: (a) ponto a; (b) ponto b; (c) ponto c.

Passo 1

Bom, para fazermos essa questão, vamos chamar de β o ângulo da linha AB.

t g β = 150 300

β = 26,565 °

Fazendo o diagrama de corpo livre da porção acima da seção abc.

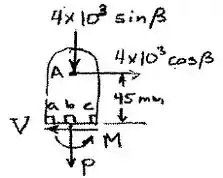
Analisando então P, V e M.

P = - 40 × 10 8 s e n β = - 1,78885 × 10 3 N

V = 4 × 10 3 c o s β = 3,5777 × 10 3 N

M = 45 × 10 - 3 4 × 10 3 c o s β = 160,997   N . m

Vamos fazer agora uma análise das proporções da seção, tranquilo?

Área:

A = 20 20 = 400   m m 2 = 400 × 10 - 6 m 2

Momento de inércia:

I = 20 20 3 12 = 13,333 × 10 3 m m 4 = 13,333 × 10 - 9 m 4

Passo 2

Com esses dados em mão podemos começar a analisar cada ponto individualmente. No ponto a teremos

σ = P A - M x I = - 1,78885 × 10 3 400 × 10 - 6 - 160,997 - 10 × 10 - 3 13,333 × 10 - 9 = 116,3   M P a

Nas extremidades nosso τ é nulo, logo para esse ponto e para o c, τ = 0

Analisando agora o ponto b

σ = P A = - 1,78885 × 10 3 400 × 10 - 6 = - 4,47   M P a

Para calcularmos o τ precisamos antes do valor de Q ,   então

Q = y - × A = 20 × 10 × 5 = 1000   m m 3 = 10 - 6 m 3  

Então τ fica

τ = V Q I t = 3,5777 10 - 6 13,333 × 10 - 6 20 × 10 - 3 = 13,42   M P a

Por ultimo mas não menos importante, para o ponto c

σ = P A - M x I = - 1,78885 × 10 3 400 × 10 - 6 - 160,977 10 × 10 - 3 13,333 × 10 - 9 = - 125,2   M P a

Na extremidade não temos τ , então

τ = 0

Resposta

a )   σ = 116 , 3     M P a

τ = 0  

b )   σ = - 4,47   M P a

τ = 13,42   M P a  

c )   σ = - 125,2   M P a

τ = 0  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga é composta por três chapas finas soldadas, como mostra a figura. Se submetida a um cisalhamento V = 48 kN, determine o fluxo de cisalhamento nos pontos A e B. Calcule também a tensão de cisalha
Selecione no Apêndice B a viga de aço de abas largas de menor peso que suportará com segurança a carga da máquina mostrada na figura. A tensão de flexão admissível é σ = 168M P a e a tensão de cisalha
As vigas do assoalho de um galpão de depósito devem ser selecionadas em função de vigas quadradas de madeira feitas de carvalho. Se cada viga tiver de ser projetada para suportar uma carga de 7,5k N /
Resolva o Problema 11.6 se a seção transversal tiver largura desconhecida, mas tiver de ser quadrada, isto é,h = b
A viga de madeira de ser carregada como mostra a figura. Se as extremidades suportarem somente forças verticais, determine o maior valor de P que pode ser aplicado. σ a d m = 25 M P a ,τ a d m = 700k