Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 136
Duas hastes estão ligadas por um bloco deslizante como mostra a figura. Desprezando o efeito do atrito, determine o binário necessário para manter o sistema em equilíbrio.
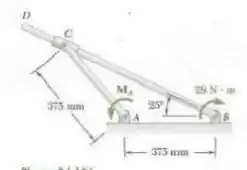
Passo 1
Ignorando o efeito do atrito devemos encontrar o vamos do momento de binário indicado na figura. Façamos primeiramente o diagrama de corpo livre para a barra obtendo o seguinte
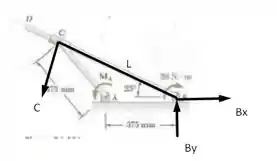
A partir desse diagrama podemos perceber que a força é perpendicular a . Aplicando as condições de equilíbrio, adotando o sentido anti-horário como positivo vamos ter
Onde , então
Passo 2
Agora fazendo o diagrama de corpo livre para a barra teremos
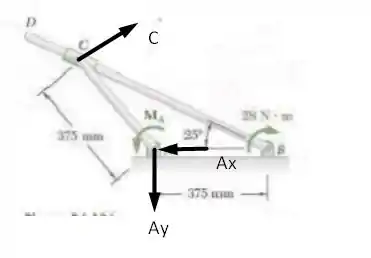
Aplicando, também, as condições de equilíbrio vamos ter
Resposta
Exercícios de Livros Relacionados
A barra esguia e uniforme de comprimento 2 r e massa m repousa contra a superfície circular, conforme mostrado. Determine a força normal no pequeno rolo A e a magnitude da reação de pivô ideal em O .
A localização indicada do centro de gravidade da caminhonete de 3600l b é para a condição sem carga. Se uma carga cujo centro de gravidade está atrás do eixo traseiro for adicionada ao caminhão, deter
Calcule a magnitude da força suportada pelo pino em A sob a ação da carga de 1,5k N aplicada ao suporte. Despreze a fricção na ranhura.
A barra esguia e uniforme de comprimento 3 r e massa m repousa contra a superfície circular, conforme mostrado. Determine a força normal no ponto de contato C e a magnitude da reação de pivô ideal em
Um mecânico está reinstalando uma lâmina recém-afiada em um cortador de grama. Um bloco de madeira encaixado em C impede a lâmina de girar quando a força de 30l b é aplicada ao cabo da chave. A lâmina