Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas Revisão - Ex. 183
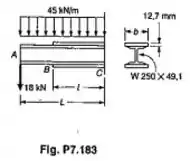
Duas placas de cobertura de de espessura são soldadas, como mostrado, ao perfil laminado da viga de comprimento Sabendo-se que e determinar: (a) a largura necessária das placas de cobertura; (b) o menor valor de permissível para as placas.
Passo 1
Fala aí galera do Responde aí, bora matar esse livro de resmat. Primeiramente, vamos calcular o momento no engaste:
O próximo passo é determinar o centroide da seção, que será:
Sabemos que:
Substituindo:
Sabemos que o perfil é conhecido e podemos obter o momento em um ábaco. Logo:
Substituindo:
Passo 2
Agora, devemos verificar o comprimento pedido. Sabemos que:
Temos que, sem as barras:
Logo:
Portanto:
Portanto:
Resposta
Exercícios de Livros Relacionados
Para a viga e o carregamento mostrado, determinar: a) máxima tensão normal numa seção transversal em C; b) a máxima tensão de cisalhamento numa transversal imediatamente à esquerda de B.
Desenhar os diagramas de força cortante e de momento fletor para a viga com o carregamento mostrado e determinar a máxima tensão normal devido à flexão.
Desenhar os diagramas de força cortante e de momento fletor para a viga com o carregamento mostrado e determinar a máxima tensão normal devido à flexão.
Desenhar os diagramas de força cortante e de momento fletor para a viga com o carregamento mostrado e determinar a máxima tensão normal devido à flexão.
Pede-se: (a) Para a viga com o carregamento mostrado e usando funções singulares, escrever as equações que definem as curvas do diagrama de força cortante e de momento fletor; (b) determinar o máximo