Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.8 - Ex. 193

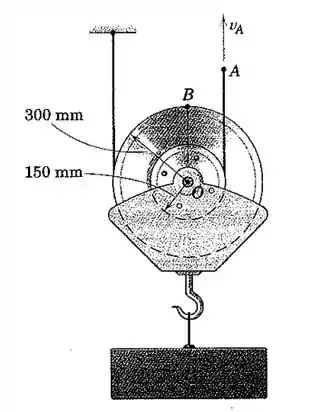
As duas polias estão presas uma na outra para formar um único conjunto rígido, e cada um dos dois cabos está enrolado firmemente em torno de sua respectiva polia. Se o ponto A no cabo de elevação possui uma aceleração para cima de 1 m/s², determine os módulos da velocidade e da aceleração dos pontos O e B se o ponto A tem uma velocidade para cima de 1,5 m/s no instante representado.

Passo 1

Bom pessoal, considerando a polia não desliza, temos que o ponto de contato da polia maior com o cabo preso no teto é o Centro Instantâneo C. Vamos fazer um esboço do mecanismo:

Podemos então calcular a velocidade e aceleração no centro das polias:

a O = 0,3 0,45 a A = 0,67 j ^   m / s 2 ( ↑ )

v O = 0,3 0,45 v A = 1 j ^   m / s ( ↑ )

Vamos também calcular a velocidade relativa entre B e O:

v B / O = ω × B O - = v O r O C k ^ × B O - j ^ = - 1 0,3 0,3 i ^ = - 1 i ^   m / s

E usando a equação da velocidade relativa:

v B = v O + v B / O = 1 j - 1 i   m / s

Seu módulo, portanto vale:

v B = - 1 2 + 1 2 = 1,414   m / s 2

Passo 2

Agora, vamos usar a equação da aceleração relativa entre os pontos B e O:

a B = a O + a B O n + a B O t

Onde:

a B O n =   ω × ω × r B O = - ω 2 r B O = - v O 2 r B O = - 1 2 0,3 j = - 3,33   j ^   m / s 2

a P O t = α × r P O = - a O i ^ = - 0,67 i ^   m / s 2

Substituindo os valores na equação, temos que:

a B = 0,67 j ^ - 3,33 j ^ - 0,67 i ^ = - 0,67 i ^ - 2,66 j ^ m / s 2

Caso queria saber o módulo:

a B = - , 67 2 + - 2,66 2 = 2,75   m / s 2

Resposta

a O = 0,67 j ^   m / s 2 ( ↑ )

v O = 1 j ^   m / s ( ↑ )

v B = 1 , 414   m / s 2

a B = 2 , 75   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A roda desliza enquanto rola. Se v O = 1,2m / s e se a velocidade de A em relação a B é de 0,9 2m / s , localize o centro instantâneo C de velocidade nula e encontra a velocidade do ponto P.
O disco circular gira em torno de seu eixo z com uma velocidade angular ω = 2r a d /s . Um ponto P localizado sobre a borda possui uma velocidade dada por v = - 0,8 i - 0,6 jm / s . Determine as coord
A cuba oscilatória de produtos do Prob. 5/86 é apresentada aqui novamente. Se a manivela OB possui uma velocidade angular constante no sentido anti-horário de 0,944 rad/s, determine a velocidade angul
22. O disco está originalmente girando a ω 0 = 8 r a d s . Se ele é submetido a uma aceleração angular constante a = 6 r a d s 2 , determine as intensidades da velocidade e das compontes n e t da acel