Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.8 - Ex. 190

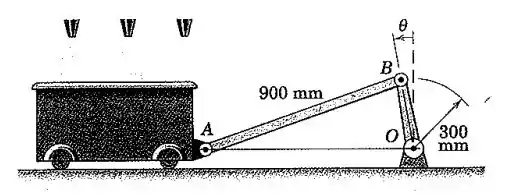
A cuba oscilatória de produtos do Prob. 5/86 é apresentada aqui novamente. Se a manivela OB possui uma velocidade angular constante no sentido anti-horário de 0,944 rad/s, determine a velocidade angular de AB quando θ = 20 ° .

Passo 1

Bom pessoal, nesta questão precisamos usar alguns truques geométricos. Veja o desenho do mecanismo representado abaixo:

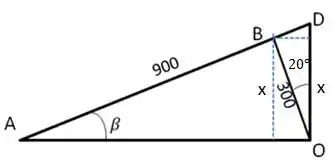
Podemos ver então que:

x = 900   s e n β = 300   c o s 20 °

s e n β = 0,313

β = 18,25 °

Agora, vamos representar os vetores velocidade.

O carrinho A se movimenta na horizontal e o ponto B possui velocidade perpendicular à haste BO. Juntando os vetores e fazendo um diagrama, temos

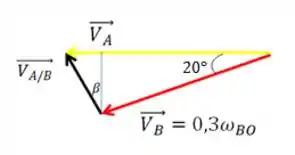
Agora, basta aplicar a Lei dos senos no triângulo acima para descobrir a velocidade angular ω B O :

V A / B s e n 20 = V B s e n 90 - β

V A / B s e n 20 = 0,3 ( 0,944 ) s e n 90 - 18,78

V A / B = 0 , 102   r a d / s

E podemos agora calcular a velocidade angular de AB:

V A / B = ω × A B

ω = 0,102 0,9 = 0,1133 r a d s ,   s e n t i d o   h o r a r i o

Resposta

ω = 0,1133 r a d s ,   s e n t i d o   h o r a r i o

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga esbelta de 3m possui uma massa de 50k g e é liberada a partir do repouso na posição horizontal em θ = 0 . Se o coeficiente de atrito estático entre o suporte fixo junto a O e a viga é de 0,30 ,
11. Se a barra AB desliza ao longo da ranhura horizontal com uma velocidade de 18 m/s, determine a velocidade angular da barra de ligação BC no instante mostrado.
Para o instante representado, o centro instantâneo de velocidade nula para a placa retangular em movimento plano está localizado em C. Se a placa possui uma velocidade angular no sentido anti-horário
A placa retangular gira em torno de seu eixo fixo z. No instante considerado sua velocidade angular é ω = 3r a d / s e está diminuindo na taxa de 6 rad/s por segundo. Para esse instante escreva as exp
O grande carretel para cabo de eletricidade é rolado para cima no plano inclinado pelo veículo conforme mostrado. O veículo parte do repouso com x = 0 para o carretel e acelera na taxa constante de 0,