Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.8 - Ex. 187
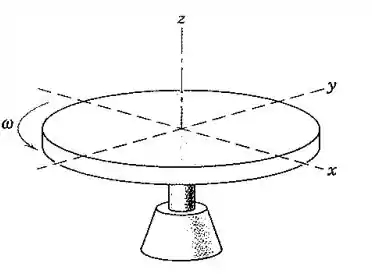
O disco circular gira em torno de seu eixo z com uma velocidade angular . Um ponto P localizado sobre a borda possui uma velocidade dada por . Determine as coordenadas de P e o raio do disco.
Passo 1
Bom pessoal, nesta questão basta utilizar os conceitos aprendidos ao longo do capítulo. A velocidade absoluta e a velocidade angular de um disco que rotacional podem ser relacionadas pela equação:
Agora basta substituir os valores e fazer o produto vetorial.
Temos então o sistema:
Logo:
Seu módulo será:
Resposta
Exercícios de Livros Relacionados
A viga I de 4,8m tem uma massa de 900k g e é mantida na posição horizontal pelo pino em O e pelo cabo vertical que passa em torno da polia em A e em torno do tambor do guincho motorizado de 200k g em
A figura mostra uma plataforma inclinável de caminhão para descarregar contêineres carregados. O contêiner carregado de 120t pode ser considerado como um bloco retangular homogêneo maciço com centro d
A barra curva de massa m é articulada ao disco que gira em O e se apoia contra um dos pinos liso A e B que estão fixados no disco. Se o disco gira em torno de seu eixo vertical C , determine a força e
A barra esbelta uniforme de massa m e comprimento l é liberada a partir do repouso na posição vertical e gira sobre sua extremidade plana em torno da quina em O . (a) Se a barra desliza quando θ = 30
O mastro uniforme de 24m possui uma massa de 300k g e é articulado em sua extremidade inferior a um suporte fixo junto a O . Se o guincho C desenvolve um torque de partido de 1300N ∙ m , calcule a for