Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.4 - Ex. 79
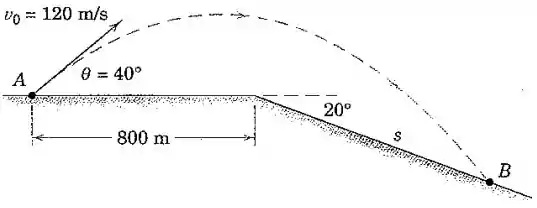
Um projétil é lançado a partir do ponto com as condições iniciais mostradas na figura. Determine a distância inclinada que posiciona o ponto de impacto. Calcule o tempo de voo .
Passo 1
Galera, pra determinar a distância , a gente precisa descobrir qual o ponto de cruzamento entre a trajetória da parábola e o piso inclinado, que será o ponto .
Então, vamos começar equacionando o movimento horizontal:
Acima e em todos os demais cálculos, consideraremos o vértice a de como a origem do sistema de coordenadas.
Para o movimento vertical, teremos:
Substituiremos a expressão de encontrada:
Passo 2
Agora que conseguimos escrever somente em função (os outros valores , e são conhecidos), temos a equação da trajetória, da parábola mostrada no desenho.
Podemos também escrever uma equação da reta formada pelo piso inclinado, olha só:
pois o coeficiente angular dessa reta seria justamente a tangente do ângulo que a reta faz com o eixo positivo, e o coeficiente linear é zero porque a reta passa pela origem do nosso sistema de coordenadas.
Então, para descobrir as coordenadas do ponto , basta igualar nas duas equações:
Para facilitar as contas, já vamos substituir , e :
Então, o ponto está à direita da origem. Olhando pra figura e usando propriedades de ângulos em triângulos retângulos, temos:
Passo 3
Pra achar o tempo de voo, voltamos naquela primeira expressão do tempo que encontramos:
Substituindo , e , obtemos: