Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 3.Problemas - Ex. 40
3.40. A mola tem uma rigidez e um comprimento não deformado de . Determine a força nos cabo BC e BD quando a mola é mantida na posição mostrada.
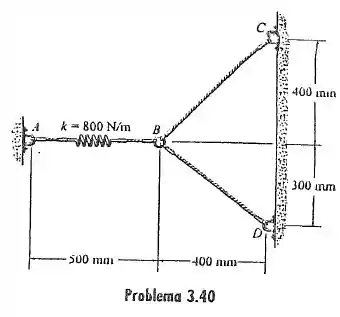
Passo 1
Fala! Queremos as forças em BD e BC.
Para resolver esse exercício usaremos as equações de equilíbrio nos eixos x e y. Por isso, vamos fazer aquele DCL fofo:
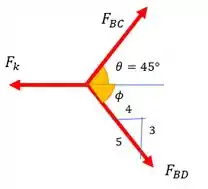
Só uma observação. Vemos que temos um triângulo retângulo 3/4/5 na inclinação de pelo triângulo que tem como hipotenusa o .
E sabemos que , porque o triângulo que tem como hipotenusa na figura tem catetos iguais.
Vamos seguir!
Passo 2
Vamos começar determinando a força da mola
Podemos determinar x sendo a posição final menos a posição da mola relaxada, ou seja, o comprimento dela na figura menos o comprimento não deformado:
Então
Passo 3
Vamos começar calculando
Isso nos dá
Agora vamos fazer o mesmo para
Passo 4
Agora podemos resolver substituindo as equações
Isso nos dá que
Logo