Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 87
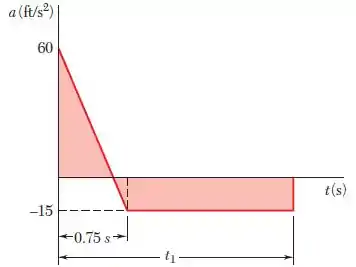
Durante o teste de um novo bote salva-vidas, um acelerômetro fixado ao bote fornece o registro mostrado na figura. Se o bote tem uma velocidade de 7,5ft/s, t = 0 e fica em repouso no tempo t1, determine, usando o método da Seção 11.8, (a) o tempo t1, (b) a distância por meio da qual o bote se move antes de entrar em repouso.
Passo 1
A área sob a curva é dividida em três regiões, conforme mostrado.
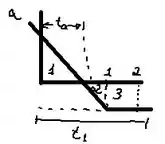
Passo 2
- Primeira nota
- Da discussão após a Eq. (11.13) e assumindo x = 0, temos
ou
Agora
Nesse caso, a integral é igual à área sob a curva a-t. Então, com v0 = 7.5 , = 0
Temos
ou
Passo 2
onde A é a área de uma região e é a distância ao seu centróide. Então para t1 = 2.375 s
Resposta
Exercícios de Livros Relacionados
Considerando uma aceleração uniforme de 3m / s ² ² e sabendo que a velocidade escalar de um carro que passa por A é 50k m / h , determine (a) o tempo necessário para que o carro alcance B , (b) a velo
A aceleração de uma partícula é definida pela relação a = - k v onde k é uma constante. Sabendo que x = 0ev = 81m / s em t = 0 ,eq u ev = 36m / s quando x = 18m , determine (a) a velocidade da partícu
Um policial em um carro de patrulha, estacionado em uma zona de 70k m / h de limite de velocidade, observa um automóvel que passa a uma velocidade lenta e constante. Acreditando que o motorista desse
Um caminhão percorre 220me m10s enquanto está sendo desacelerado a uma taxa constante de 0,6m / s ² ². Determine (a) sua velocidade inicial (b) sua velocidade final, (c) a distância percorrida durante
Partindo de x = 0 sem velocidade inicial, uma partícula sofre uma aceleração a = 0,8 v 2 + 49 , onde aev são expressos em m / s ² ² e m / s , respectivamente. Determine (a) a posição da partícula quan