Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 20.Problemas - Ex. 11
O cone rola em um círculo e gira em torno do eixo a uma taxa constante . Determine a velocidade e a aceleração angular do cone se ela rola sem deslizar. Além disso, qual é a velocidade e a aceleração no ponto ?
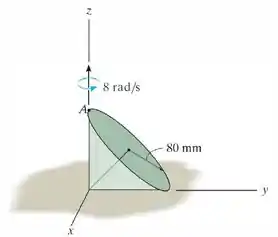
Passo 1
O DCL abaixo mostra as velocidades e acelerações presentes no problema.
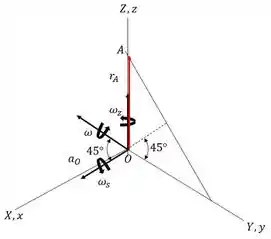
No instante mostrado na figura, o sistema fixo coincide com o sistema rotativo . Uma vez que o disco rola sem escorregar, sua velocidade angular é sempre direcionada para o eixo . Logo,
Calculando na componente k:
E na componente j:
Portanto,
Passo 2
Uma vez que encontra-se sempre no plano , nota-se que tem uma direção constate em relação ao sitema , se esse estiver girando em torno de . Assim,
Passo 3
Como , a velocidade no ponto será
E a aceleração no ponto é igual a
Resposta
Portanto, a velocidade e a aceleração angular sem a roda deslizaré são iguais a e . E a velocidade e a aceleração no ponto , no instante em que , são iguais a e , respectivamente.