Enunciado
Mecânica e Resistência dos Materiais - Dinamica Classica de Particulas e Sistemas - Marion- Ed: 5º - Capítulo 2.Problemas - Ex. 31
No Exemplo 2.10, a velocidade inicial da partícula carregada entrante não tem nenhuma componente ao longo do eixo . Demonstre que, mesmo se ela tivesse uma componente , o movimento subsequente da partícula seria o mesmo, com alteraçáo somente do raio da espiral.
Passo 1
Faala meu povo, bora com tudo pra mais uma questão do nosso livro!
Primeiramente vamos pegar o exemplo 2.10 do nosso livro:
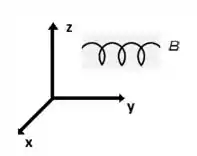
A partir da equação 2.78, temos:
A projeção da hélice no plano é um círculo.
Comparando com a equação da circunferência, dada por:
Portanto o raio do círculo no plano é:
Agora substituindo , temos:
Finalizamos aqui nossa questão, tudo beleza? Te vejo na próxima!
Resposta
Exercícios de Livros Relacionados
O deslocamento vertical do cilindro A em metros é dado por y = t 2 / 4 onde t é expresso em segundos. Calcule a aceleração descendente de a B do cilindro B . Identifique o número de graus de liberdade
Uma massa q de areia é descarregada por unidade de tempo por um transportador de correia movendo-se com velocidade v0. A areia é desviada por uma placa em A de tal forma que cai em um fluxo vertical.
Uma pequena bola de massa presa no ponto médio de um cordão elástico bem esticado de comprimento que posso deslizar em um plano horizontal. A bola recebe um pequeno deslocamento em uma direção perpend
O movimento de uma partícula carregada em um campo eletromagnético pode ser obtido pela equação de Lorentz para a força sobre uma partícula nesse tipo de campo. Se o vetor do campo elétrico é E e o ve