Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 83
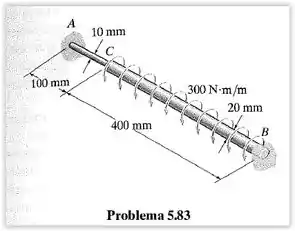
O eixo de aço A-36 é composto por dois segmentos: , com diâmetro de e , com diâmetro de . Se o eixo estiver engastado em suas extremidades e e for submetido a um torque distribuído uniforme de ao longo do segmento , determine a tensão de cisalhamento máxima absoluta no eixo.
Passo 1
Olá, pessoal! Tudo bem com vocês?
O enunciado pede que encontremos o torque nos apoios e e a tensão de cisalhamento máxima absoluta no eixo. Ele nos dá as seguintes informações:
Aço A-36, portanto
Vamos construir o nosso diagrama de corpo livre:
Fazendo o somatório das forças, temos:
O valor do carregamento aplicado na seção é , podemos então encontrar o valor do torque que atua na metade do segmento. Calculamos usando a área do retângulo, :
Passo 2
Fazemos então um corte no segmento , a uma distância de . Como o torque é distribuído linearmente por todo esse segmento, então podemos calcular , multiplicando pela distância :
Passo 3
Como o eixo está fixo nas duas extremidades, sabemos que o ângulo de em relação a vai ser nulo.
Como a região onde o ângulo é zero fica no segmento , o torque vai provocar um ângulo de torção tanto no segmento , quanto no segmento . Portanto, temos:
Sendo que o momento polar de inercia, J, é dado por:
Substituindo:
Substituindo na expressão que encontramos fazendo o somatório dos momentos:
Passo 4
A tensão máxima vai ocorrer no segmento , que é o segmento do carregamento. Logo: