Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 69

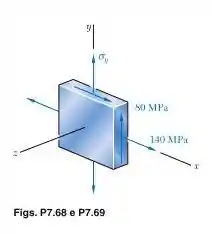
Para o estado de tensão indicado, determine a tensão de cisalhamento máxima quando (a) σ y = 20   M P a e (b) σ y = 1 4 0   M P a .   (Sugestão: Considere as tensões de cisalhamento no plano e fora do plano de tensões).

Passo 1

Fala aí, galerinha. Tudo bem com vocês? Bora matar esse livro.

O primeiro passo é listar os dados fornecidos pelo problema. Sabemos que, para a letra a:

σ x = 140   M P a

σ y = 20   M P a

τ x y = 80   M P a

Como a tensão máxima de cisalhamento é o raio do círculo de Mohr, temos que achar este raio.

Portanto, temos que achar o centro do círculo, que é dado pela média das tensões:

σ m é d = 1 2 σ x + σ y = 8 0   M P a

Sabemos que, o raio é dado por:

R = σ x - σ y 2 2 + τ x y 2 = 100   M P a

Logo, a tensão máxima no plano será::

τ m á x = R = 100   M P a

Precisamos agora verificar a tensão máxima fora do plano, para ver qual é maior. Para isso, precisamos da tensão máxima e mínima. Elas serão:

σ m á x = σ m é d + R = 180   M P a

σ m i n = σ m é d - R = - 20   M P a

Logo, a tensão fora do plano será:

τ m á x = 1 2 σ m á x - σ m í n

τ m á x = 100   M P a

Logo, a tensão máxima é:

τ m á x = 100   M P a

Passo 2

Para a letra b, será o mesmo procedimento, mas teremos:

σ x = 140   M P a

σ y = 1 4 0   M P a

τ x y = 80   M P a

Portanto, temos que achar o centro do círculo, que é dado pela média das tensões:

σ m é d = 1 2 σ x + σ y = 140   M P a

Sabemos que, o raio é dado por:

R = σ x - σ y 2 2 + τ x y 2 = 80   M P a

Logo, a tensão máxima no plano será::

τ m á x = R = 80   M P a

Precisamos agora verificar a tensão máxima fora do plano, para ver qual é maior. Para isso, precisamos da tensão máxima e mínima. Elas serão:

σ m á x = σ m é d + R = 220   M P a

σ m i n = 0

Logo, a tensão fora do plano será:

τ m á x = 1 2 σ m á x - σ m í n

τ m á x = 110   M P a

Logo, a tensão máxima é:

τ m á x = 110   M P a

Resposta

  1. τ m á x = 100   M P a
  2. τ m á x = 110   M P a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barra retangular em balanço está sujeita à força de 25 kN. Determine as tensões principais no ponto A.
Um ponto sobre uma chapa fina está sujeito a dois estados de tensão sucessivos como mostra a figura. Determine o estado de tensão resultante com referência a um elemento orientado como mostrado na par
A haste curva tem diâmetro de 15 mm e está sujeita à força de 600 N. Determine as tensões principais e a tensão de cisalhamento máxima no plano desenvolvidas no ponto A e no ponto B. Mostre os resulta
As componentes da deformação em um ponto sobre a parede de um vaso de pressão são ε x = 350 ( 10 - 6 ) , ε y = - 460 ( 10 - 6 ) , γ x y = - 560 ( 10 - 6 ) e ε z = 0 . Determine (a) as deformações prin
Resolva o Problema 10.8 usando o círculo de Mohr.