Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.8 - Ex. 53

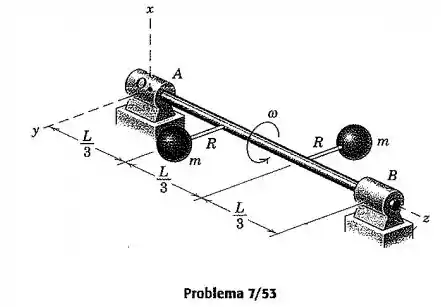
O eixo esbelto sustenta duas partículas deslocadas cada uma de massa m e gira em relação ao eixo z com uma velocidade angular ω conforme indicado. Escreva uma expressão para a quantidade de movimento angular H do sistema em relação à origem O dos eixos x - y - z para a posição mostrada. Escreva a energia cinética T do sistema por inspeção e verifique seu resultado aplicando a Eq. 7/18.

Passo 1

Para resolver esse exercício vamos usar os conceitos do tensor de inércia e energia cinética. Para começar iremos encontrar o valor de H e depois aplicar na energia cinética.

Passo 2

Vamos começar coletando todos os dados que temos. Pelo problema vemos que apenas teremos velocidade angular no eixo z , portanto H ficará da seguinte forma:

H = ω ⋅ - I x z ⋅ i ^ - I y z ⋅ j ^ + I z z ⋅ k ^

Agora usando a simetria do problema, temos que os momentos de inércia para cada componente serão:

I x z = 0

I y z = m ⋅ R ⋅ l 3 - m ⋅ R ⋅ 2 ⋅ L 3 = - m ⋅ R ⋅ l 3

I z z = 2 ⋅ m ⋅ R 2

Assim, H = m ⋅ R ⋅ ω ⋅ l 3 ⋅ j ^ + 2 ⋅ R ⋅ k ^ .

Agora utilizando a equação da energia cinética para o problema, teremos que:

T = 1 2 ⋅ ω ⋅ H 0 = 1 2 ⋅ ω ⋅ k ^ ⋅ m ⋅ R ⋅ ω l 3 ⋅ i ^ + 2 ⋅ R ⋅ k ^ = m ⋅ R 2 ⋅ ω 2

Pois o produto escalar de i ^ ⋅ k ^ = 1 ⋅ 1 ⋅ cos ⁡ 90 º = 0 .

Resposta

Resposta: H = m ⋅ R ⋅ ω ⋅ l 3 ⋅ j ^ + 2 ⋅ R ⋅ k ^

T = m ⋅ R 2 ⋅ ω 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O disco de 20 kg A é fixado ao bloco B de 10 kg utilizando o sistema de cabo e polia mostrados. Se o disco rola sem deslizar, determine sua aceleração angular e a aceleração do bloco quando eles são s
A montagem consiste em uma disco de 8 kg e uma barra de 10 kg que está conectada ao disco por um pino. Se o sistema é solto do repouso, determine a aceleração angular do disco. Os coeficientes de atri
A montagem consiste em uma disco de 8 kg e uma barra de 10 kg que está conectada ao disco por um pino. Se o sistema é solto do repouso, determine a aceleração angular do disco, se a barra for removida
O cilindro de 7,5 Kg está inicialmente em repouso sobre uma placa de 2,5 kg. Se um momento de binário M = 60N ∙ m for aplicado ao cilindro, determine a aceleração angular do cilindro e o tempo necessá
Determine o coeficiente de atrito estático mínimo entre o disco e a superfície no Problema 17.114, de maneira que o disco role sem deslizar. Despreze a massa das polias