Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas - Ex. 98
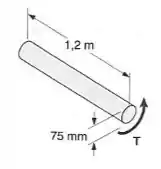
O eixo maciço mostrado é feito de um aço doce, que é considerado ser elastoplástico com e . O toque é aumentado até que o eixo tenha sido torcido de , e é então removido. Determine a intensidade e onde ocorre a máxima tensão residual de cisalhamento no eixo.
Passo 1
No item a) para descobrirmos a tensão máxima que age na nossa estrutura, precisamos antes saber a máxima tensão que a nossa estrutura suporta, e para isso a nossa fórmula é dada por:
Sabemos pelo enunciado que:
Substituindo teremos que:
Como temos o ângulo em que a nossa barra é girada, podemos usar a seguinte equação para nos ajudar:
Como todos esses dados nós já temos, podemos substituir na nossa equação, sendo assim teremos que:
Outra coisa que podemos definir é a máxima deformação elástica que a nossa barra pode ter, e para isso podemos usar a seguinte equação:
E agora podemos fazer a seguinte relação
Como uma das coisas pedidas é a posição que ocorre a máxima tensão residual, podemos substituir o nosso raio e assim teremos que:
Então a posição que a tensão máxima ocorre é no raio elástico dada por
Com esses dados podemos calcular o nosso torque que age na barra, sendo assim teremos que:
Passo 2
Se temos o raio total e o raio elástico, podemos calcular as tensões cisalhantes na superfície e na posição do raio elástico, sendo assim teremos que:
- (A máxima tensão residual de cisalhamento)
- (tensão residual de cisalhamento)
Substituindo nas equações teremos que:
Substituindo nas equações teremos que:
Passo 3
E agora podemos calcular as tensões residuais, da seguinte maneira:
A tensão residual máxima é a maior das duas acima, sendo assim teremos que:
Resposta
A máxima tensão residual de cisalhamento
E a posição que ela ocorre é dada por: